The word “tangent” actually means “to touch”. The Latin word given for the same is “tangere”. In general, we can say that any line that intersects the circle exactly at a single point on its circumference and will never enter the circle’s interior is called tangent. One circle can have many tangents. And all are perpendicular to the radius. We will learn a bit more about the tangent meaning and theorems in this given article.
Tangent Meaning
In geometry, we can say a tangent is the line actually drawn from an external point and that will pass through a point on the curve or the circumference of the given circle. One very real-life example or natural example of a tangent is, when we ride a bicycle, then every point on the circumference of the wheel actually makes a tangent with the road. Let us understand or learn the concept of a tangent with an example.
Tangent Definition: In geometry, Tangent is actually defined as a line that touches a curve or a curved surface of given figure exactly at one point.
Tangent of a Circle
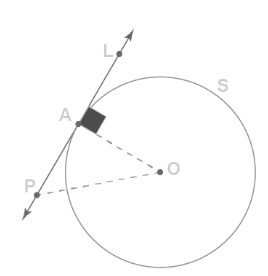
A tangent of a circle can be defined very easy as a straight line that mainly touches or intersects the circle at only one point. A tangent is that line which never enters the circle’s interior. The following given figure shows a circle with a point P. A tangent L that actually passes through P has been drawn. This is a perfect example of a tangent to circle.
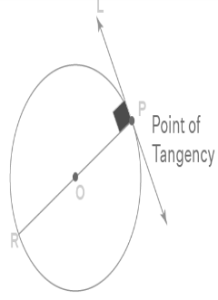
Point of Tangency
The point of tangency can be defined as the only point of intersection where the straight-line actually touches or intersects the circle. In the above given figure, point P mainly represents the point of tangency.
Tangent Properties
The tangent has mainly two important properties, which are given below: –
- A tangent always touches a curve at only one point.
- A tangent is that line that will never enter the circle’s interior.
- The tangent always touches the circle’s radius at a point of tangency at a right angle.
Apart from the above-given properties, a tangent to the circle has also mathematical theorems associated with it and those theorems are always used while doing major calculations in geometry. Let us understand a few tangents to circle theorems in more detail.
Tangent Theorems
There are two very important theorems given on the tangent of a circle. Those are the tangent to radius theorem, and the other one is the two tangents theorem. Let us discuss first, their statements and proof in detail.
Tangent Radius Theorem: The tangent at any point of a circle or the circumference of circle is perpendicular to the radius through the point of contact.
Given: Here Tangent PL to a circle S (with the center of circle O given), and the point of contact is A.
To prove: Here, we have to prove that OA is perpendicular to the tangent PL.
Proof: In the above figure, we see that point P lies outside the circle. When P & O are joined, we get PO > OA (radius of a circle). And here we see that this condition will apply to every point on the line PL except point A.
PO > OA proves that OA is actually the shortest of all the distances of point O to the other points on PL.
Hence, it is proved that OA is perpendicular to PL.
Two Tangents Theorem: Suppose that, there are two tangents are drawn to a circle from an exterior given point C.
As we know that, the Tangent theorem states the following:
- The lengths of these two tangents actually will be equal, that is, CA = CB.
- The two tangents will form an equal angles at the center, that is, ∠COA = ∠COB.
- The angle between the tangents will be always bisected by the line, joining the exterior point and the center, that is, ∠ACO = ∠BCO.
Proof: Here, all the above parts will be proved, if we show that ΔCAO is congruent to ΔCBO. And by comparing the two triangles, we see that:
- OA = OB (which is the radii of the same circle)
- OC = OC (that is common side)
- ∠OAC = ∠OBC = 90° (As we learnt above that, Tangent drawn to a circle is perpendicular to the radius at the point of tangency)
- Thus, by the RHS criterion, it is proved that, ΔCAO is congruent to ΔCBO, and the truth of all the above three assertions follows.
Let us take one example to understand, how to use the above Tangent theorem: –
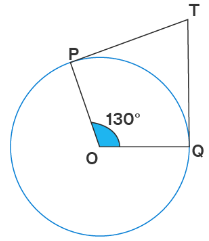
TP and TQ are the two given tangents to a circle with center O such that ∠POQ = 130°, then find angle ∠PTQ.
Solution:
Here, it is given in the question that TP and TQ are tangents.
By using the tangent radius theorem, if we draw the radius to the tangents TP and TQ, then the radius will be perpendicular to these tangents.
Thus, we found that OP is perpendicular to TP and QO is also perpendicular to TQ.
Its mean,
∠OPT = 90°
∠OQT = 90°
We also know that the sum of interior angles of a quadrilateral is 360°.
Therefore, ∠POQ + ∠PTQ + ∠OPT + ∠OQT = 360°
or, ∠PTQ = 360° – (130° + 90° + 90°)
Therefore, ∠PTQ = 50°
Conclusion:
- Only one point on the tangent intersects the circle or its boundary.
- Only one point is touched by any tangent on a circle.
- The tangent always touches the circle’s radius at a point of tangency at a right angle.
- The angle between the tangents will be always bisected by the line, joining the exterior point and the center.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out