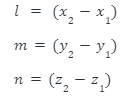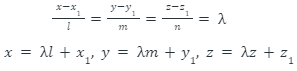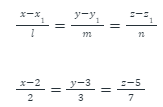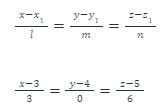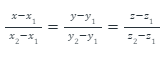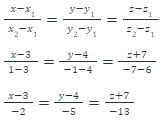Equation of a Line on a Cartesian Plane

A line is a one-dimensional figure that only has length; it has no width. The cartesian plane allows the representation of the equation of a figure in three-dimensional analysis. The x-axis, y-axis, and z-axis represent the equation of a line on a cartesian plane.  

The most basic form of the cartesian equation of a line is of the vector form:

 A→= xi→+yk→+xk→

We can also represent this expression as A(x, y, z). The x, y, and z coordinates represent the coordinates of the line. Let us learn about the equation of a line on a cartesian plane.  

Equation of a Line on Cartesian Plane

The standard form of the equation of a line is as below: 

y=mx+c

Here, m is the slope of the line, and c is the y-intercept. We can represent the equation of the line in vector form. In vector form, we get the direction of the line as well.  

For writing the equation of a line in the cartesian form, let us understand this with one example. Suppose two coordinates of a line are  (x1, y1, z1) and (x2, y2, z2). 

To calculate the equation of a line on a cartesian plane, we follow the steps below:

• Calculate Direction Ratios

To calculate the direction ratios, we simply determine the difference between the coordinates of the corresponding points. 

l, m, and n are the direction rations. 

• For the next step, we take either of two points. Let us take (x1, y1, z1).

• Substituting all the values in the cartesian form of a line:

The above is the general case of the cartesian equation. The parametric form is as below:

Therefore, the coordinates of a line are given as:

(l+x1, m+y1, z+z1)

Illustration: A straight line passes through two given points, A (2, 3, 5) and B (4, 6, 12), then find the equation of a line in cartesian form.

Solution: We have  A (2, 3, 5) and  B (4, 6, 12)

l = (4 – 2) = 2

m = (6 – 3) = 3

n = (12 – 5) = 7

Let us choose one point, say point A (2, 3, 5).

Substituting the values in the standard form of the cartesian equation of a line, we get:

This expression is the required equation of a line in the cartesian plane. 

Illustration: What are the direction ratios of a line with coordinates P (2, 4, 6) and (3, 5, 4)?

Solution: The direction ratios of the line are:

l = (x2-x1) = (3-2)=1

m=(y2-y1) = (5-4)=1

n=(z2-z1)= (4-6) = -2

Hence the direction ratios are <1,1,-2>

Illustration: A straight line passes through the two fixed points in the 3-dimensional whose position coordinates are P (3, 4, 5) and Q (6, 4, 11), then what is its cartesian equation using the two-point form?

Solution: We have  P (3, 4, 5) and Q (6, 4, 11), then the direction rations will be:

l = (6 – 3) = 3

m = (4 – 4) = 0

n = (11 – 5) = 6

Let us choose one point, say the point P (3, 4, 5).

Substituting the values in the standard form of the cartesian equation of a line, we get:

This expression is the required equation of a line on a cartesian plane. 

Equation of a Line on Cartesian Plane Passing Through Two Points

The cartesian equation of a line passing through two given points is:

Illustration: What is the cartesian equation of a line passing through P (3, 4, -7) and Q (1, -1, 6).

Solution: Let us substitute the values of P and Q in the standard form of cartesian equation of a line. 

Conclusion

If we know the coordinates of a line, we calculate its equation in various forms. The line is a one-dimensional geometric figure, but we can represent it in various forms such as:

• Standard form: y=mx+c

• Cartesian form: x-x1l=y-y1m=z-z1n

• Vector form:  A→= xi→+yk→+xk→

In this study material notes, we learned how to find a line equation on a cartesian plane. The cartesian plane helps to represent the equation of a line or point in a three-dimensional plane with the x-axis, y-axis, and z-axis.