Profile
Settings
Refer your friends
Sign out
A hyperbola is a smooth curve in space that has two connected components or branches that are mirror images of each other and resemble two infinite bows. A hyperbola is a set of points with a constant difference in distance between two foci. When you cut a double cone vertically, you get a hyperbola as a mathematical shape. Many people learn about this shape in high school or college algebra classes, but it is not clear why this shape is important. The hyperbola has a few characteristics that allow it to be useful in the real world. Hyperbolas are used in many fields to design and predict phenomena.
Hyperbola
A hyperbola is a smooth curve that lies in a plane and is described by its geometric properties or by equations for which it is the solution set in mathematics. A hyperbola is made up of two parts, known as connected components or branches, that are mirror reflections of one another and resemble two infinite bows. The intersection of a plane with a double cone forms the hyperbola, one of three types of conic sections. (The parabola and ellipse are the other conic sections.) An ellipse is a specific instance of a circle.) The conic is a hyperbola if the plane overlaps both parts of the double cone but does not pass through the apex of the cones.
Hyperbolas can appear in a variety of ways:
- the Cartesian plane, as the curve representing the function y(x)=1/x,
- as the route traced by the shadow of a sundial’s point,
- as the shape of an open orbit (as opposed to a closed elliptical orbit), such as a spacecraft’s orbit during a gravity-assisted swing-by of a planet or, more broadly, any spacecraft travelling faster than the nearest planet’s escape velocity,
- as if it were a single-apparition comet’s course (one travelling too fast ever to return to the solar system),
- represents a subatomic particle’s scattering trajectory (acted on by repulsive instead of attractive forces but the principle is the same),
- When the difference between distances to two sites, but not the distances themselves, can be computed in radio navigation,
and so on.
Each hyperbola branch has two arms that become straighter (lower curvature) as they move away from the centre. One branch’s diagonally opposing arms tend to converge on a single line, known as the asymptote of the two arms. As a result, there are two asymptotes, one of which intersects at the hyperbola’s centre of symmetry, which can be thought of as the mirror point around which each branch reflects to generate the other branch. The two coordinate axes are the asymptotes in the case of the curve y(x)=1/x.
Hyperbola Equation
The general equation of a hyperbola is represented by the equation below. The x-axis represents the hyperbola’s transverse axis, and the y-axis represents the hyperbola’s conjugate axis.
Hyperbola Shape
A hyperbola intersecting a plane with both halves of a double curve yields a two separate curve. The plane need not be parallel to the cone’s axis; the hyperbola will be symmetrical irrespective.
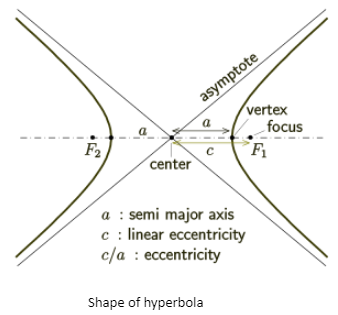
You can see the following in the above diagram:
- A symmetrical axis (that goes through each focus)
- Two points of intersection (where each curve makes its sharpest turn)
- Two asymptotes that are not part of the hyperbola but show where the curve would go in each of the four directions if it were continued indefinitely
- In addition, there is another axis of symmetry that runs through the middle of the hyperbola and separates the two branches
Conclusion
The hyperbola has a few characteristics that allow it to be useful in the real world. Hyperbolas are used in many fields to design and predict phenomena. The task of locating a point based on differences in its distances from other points or, to put it another way, the difference in distances between two points. Arrival times of co – ordinated signals between the point and the given points is solved using a hyperbola.
