Distance Between Parallel Lines Formula

Distance between two lines is how far the two lines are from each other or how far apart they are. There are lines when two points are connected with the smallest distance between them, and both ends of a line go on to infinity. We can find the distance between two sequences by measuring the distance between them when they meet. We usually figure out how far apart two lines are by measuring how far apart they are from each other.

Also, for two lines that don’t meet, the shortest distance between them is the distance that is the farthest of all the spaces between two points on each line. Let’s learn more about the distance between two bars, look at a few solved examples, and practice questions about how far two lines are apart.

Distance between two lines

Two points on the lines determine how far apart the two lines are. Two straight lines cross each other. The distance between them is the smallest distance between any two points on the lines. People often use a variety of lines to measure the distance between two lines, like a straight line or a line that is a little off. Distance between two lines is the distance from any point on one line to another point on that line at any point on that line. Eventually, the distance between two lines that meet is zero. How far apart two skew lines are is determined by the length of the perpendicular that joins them.

Distance between parallel lines

Parallel lines are farthest apart if the length of their vertical segment is less than or equal to their distance from each other. In this case, it doesn’t make a difference which line you choose, as long as the two points on each line are on the lines. Between two parallel lines, there are always many different ways for them to go in the opposite direction.

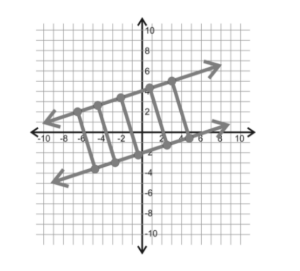
The black parts are of the same length. So, when you pick a vertical segment, make sure to pick one with endpoints that are integers, like a line.

Shortest distance between two lines

Seeing two lines in vector form as if they were:

v1 = a1 + c * b

v2 = a2 + d * b

When it comes to these two things, they are always the same.

= b = both v1 and v2 are in the same direction.

One of them is called a1, and the other is called a2. These are the coordinates of a point on v1 or v2.

To get to the end, you’d have to walk this far. The answer is: |bx (a2–a1) | / |b|

Calculating the distance between parallel lines

Take a look below and figure out how far apart the two lines are that are parallel.

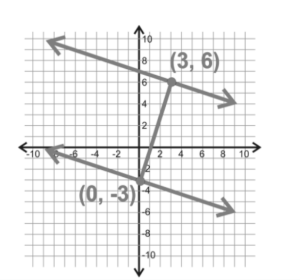
You need to figure out the slope of the two lines. Because they are next to each other, they both have the same slope, so you have both if you find the slope of one.

When you start at the y-intercept of the top line, number 7, When you get to the line again, you’d go down 1 and over 3. This means that the slope is 13, and the slope of the perpendicular direction would be 3.

In the next step, find two points on the lines. Let’s look at the y-intercept of the bottom line, which is the point where the two lines meet (0, -3); to get to the second line, rise 3 and go over 1. You could do this three times and hit the top line (3, 6). Use these two points in the distance formula to figure out how far apart the lines are from each other.

The shortest distance between two skew lines

To figure out the formula for figuring out the shortest distance between two skew lines, we must remember what skew lines are. It is possible to have skewed lines in the multidimensional system, where two lines are not parallel but never cross with each other. If you want to do this, you have to do it in three dimensions.

These lines don’t meet at any point, but they also don’t go in the same direction. They are called agonic lines, and most of the time, these lines are in three or more places. There is a general way to figure out how far two skew lines of the form l 1 = a 1 + tb 1 and l 2 = a 2 + tb 2.