Differentiation of the trigonometric functions is the technique of determining the derivatives of trigonometric functions. In other words, finding the rate of change of a trigonometric function with respect to a variable is the differentiation of trigonometric functions. The differentiation formulas for the six trigonometric functions can be applied in a variety of derivative application issues.

The sine (sin x), cosine (cos x), secant (sec x), tangent (tan x), cotangent (cot x),and cosecant (cosec x) are the six basic trigonometric functions. The derivatives of trigonometric functions will be discussed in this article. Differentiation of trigonometric functions has applications in a variety of domains, including electronics, computer programming, and cyclic function modeling.

Differentiation of trigonometric functions

Differentiation of trigonometric functions is a mathematical procedure that determines the rate of change of trigonometric functions with respect to a variable angle in trigonometry. The quotient rule can be used to differentiate trigonometric functions using the derivatives of sin x and cos x. The following are the differentiation formulas for the six trigonometric functions:

  • d( sin x)/dx = cos x
  • d( cos x)/dx = -sin x
  • d( tan x)/dx = sec2 x
  • d( cot x)/dx = -cosec2 x
  • d( sec x)/dx = sec x.tan x
  • d( cosec x)/dx  = -cosec x.cot x

Now Let us Proof the Derivatives of Trigonometric Function:

  • Derivative of Sin x

We’ll use the first principle of differentiation to find the derivative of sin x, which is the definition of limits.

We know that: sin (P+Q) = sin P cos Q + sin P cos Q

Now let us Differentiate the trigonometric Function, Sin x.

der1

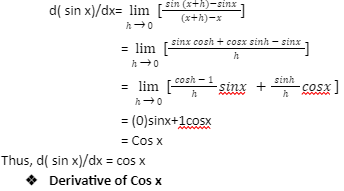
We’ll use the first principle of differentiation to find the derivative of sin x, which is the definition of limits.

We know that: cos (P + Q) = cosP cos Q – sin P sin Q

Now let us Differentiate the trigonometric Function, cos x.

der2

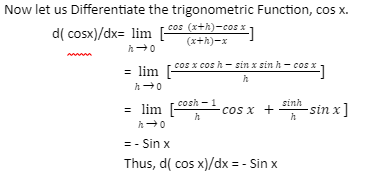
Derivative of Tan x

Using the quotient rule, we’ll find the derivative of tan x. To calculate the derivative, we’ll use the basic trigonometric formulas and identities;

We know that, d( sin x)/dx = cos x and d( cos x)/dx = -sin x 

der3

Similarly we can also prove the differentiation of other Trigonometric Function.

Application of Derivatives of Trigonometric function

Differentiation of trigonometric functions has a wide range of applications in mathematics and in everyday life. The following are a some of them:

  • It’s used to figure out how steep the tangent line to a trigonometric curve y = f is (x).
  • It is used to find the slope of a trigonometric curve y = f’s normal line (x).
  • It aids in determining the equation of a curve’s tangent or normal line.
  • Differentiation of trigonometric functions is used in a variety of industries, including electronics, computer programming, and modeling various cyclic functions.
  • To get the maximum and lowest values of a function, we use the derivatives of trigonometric functions.

Differentiation Can also be used to 

  • Find Increasing Decreasing Function:  An increasing function is one in which if x1 > x2, then f(x1) > f(x2), meaning that as x increases, so does f(x). A decreasing function is one that gets smaller as x gets bigger. A function may, of course, be increasing in some locations while decreasing in others. A turning point is a moment at which a function switches from increasing to decreasing or vice versa. A stationary point is a form of turning point. Differentiation can be used to assess if a function is increasing or decreasing. If the derivative of a function is always positive, the function is rising. If the derivative of a function is always negative, the function is declining.
  • Maxima Minima of any Function: Although the gradient is the same (= zero) at all stationary places, it is frequently vital to determine if you have located a maximum point, a minimum point, or a point of inflexion. As a result, the gradient on either side of the stationary point must be examined (alternatively, we can use the second derivative). The gradient is positive just before the maximum, zero at the maximum, and negative immediately after the maximum at maximum points. The gradient is negative at the lowest locations, then zero, then positive. Finally, the gradient can be positive, zero, positive or negative, zero, negative at points of inflexion.

Point To Remember

  • The following are the differentiation formulas for the six trigonometric functions:
  • d( sin x)/dx = cos x
  • d( cos x)/dx = -sin x
  • d( tan x)/dx = sec2 x
  • d( cot x)/dx = -cosec2 x
  • d( sec x)/dx = sec x.tan x
  • d( cosec x)/dx  = -cosec x.cot x