Combined two functions

Combining two functions is the process through which we add, subtract, multiply or divide two functions together to make a new function. Combinations of functions are as easy as adding numbers.

All four operations of combinations of functions are explained below.

1. Sum 

(f+g)(x)=f(x)+g(x)

For example: f(x)=2X+1, g(x)=3X+4

(f+g)(x)=f(x)+g(x)=(2X+1)+(3X+4)=5X+5

You can also evaluate these functions by particular inputs such as X = 2

Let’s say h is the new function. So we have:

h(x)=f(x)+g(x)=5X+5

Evaluating the above function for x = 2

Case 1: Substitute the value of x in combined function

h(x)=5X+5

h(2)=5(2)+5=15

Case 2: Find f(x) and g(x) and add them 

f(x)=2X+1

f(2)=2(2)+1 = 5

g(x)=3X+4

g(2)=3(2)+4=10

f(2)+g(2)=5+10=15

By substituting x = 2 into the functions, they both gave us the same answer. 

2. Difference

(f-g)(x)=f(x)-g(x)

The domain of combinations of functions

The domain of an arithmetic combination function f and g consists of all real numbers common to the domain of f and g.

For example, the plus sign in f + g is the part of the function name that assigns to each x the sum of two numbers, f(x) + g(x).

Solved examples

Example 1: Combining functions: If f(x)=4x-6 and g(x)=2×2- 3x, what will be the equation for (a) f-g and (b) fg and the domain of each? 

Solution

1.  (f-g)(x)=f(x)-g(x)=(4x-6)-(2×2-3x)= -2×2+7x-6

The domain is the set of real numbers. 

2. (fg)(x)=f(x)g(x)=4x-62×2-3=2(2x-3)x(2x-3) 

(fg)(x)=2x, where the domain is {x⏐x0 and x3/2}

Composition of functions 

This is just another type of combination called composition. Composition is the process of applying one function to another function. This function is denoted by a simple small circle (), which lies between the functions. For example: (fg)=f {g(x)}

This function will be read as f composed with g of x.

Example: Example of equal composition. If f(x)=3x-8 and g(x)=x + 83

Find the equation for 

1. fg

2. gf

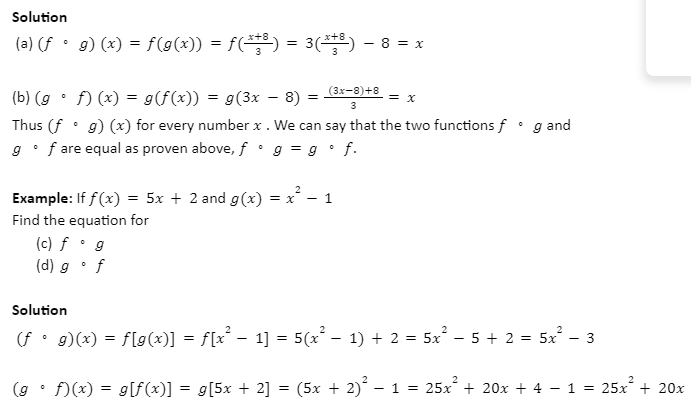
Finding domains on the composition of functions

You need to find two domains because finding a composition of functions, x is not the one being plunged into the other function. Instead of x, it is the inner function evaluated at x. Consider (fg)(x), and you will see that g is evaluated to x and not the other way around. Therefore, x has to be in the domain of g. You must have also noticed that f is evaluated at g(x). Thus g(x) is in the domain of f. 

Example: Equation f(x)=(x-2) and g(x)=  In (1+x2), find (gf)(x)

Example: If f(g(x)) and g(f(x)) are equal for all x, equation f(x)=kx-4 and g(x)=kx+6, find the value of k.

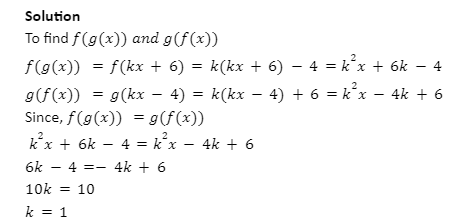
Conclusion 

In this section, we learned about the combination of functions and composition of functions and how to find their domains. We saw how two parts are combined using different processes and clarified how the combination and composition of functions work with some solved examples. Combinations of functions are straightforward problems to solve compared to the composition of functions. Still, once the concept of composition is clear, both topics will be easy to do. Always remember to solve the composite functions using BODMAS, that is, by simplifying the elements within the brackets and then moving forward to solve the equation.