Profile
Settings
Refer your friends
Sign out
It is a selection of all or a part of a set of objects without considering the order in which the objects might be selected. For example, let’s take the three letters – A, B, and C – and select two letters at a time to make a combination. This combination has three possible selections: AB, BC, or AC. (Note: AB and BA are considered one combination as the order in which it is selected does not matter. This is what differentiates Combination from Permutations).
Distinction Between Combination and Permutation:
A combination focuses on selecting objects, irrespective of the order in which they are chosen. In permutations, the arrangement of objects concerning their order of selection is of focus.
Formula
To calculate the number of combinations of n objects taken r at a time is:
nCr = n(n – 1)(n – 2) … (n – r + 1)/r!
nCr = n! / r!(n – r)!
nCr = nPr / r!
Linear Combination of Vectors
A vector V can be a linear combination of other vectors U and W if it can be represented as the sum of scalar multiples of other vectors U and W.
Example:
If a = 4b + 5c as below,
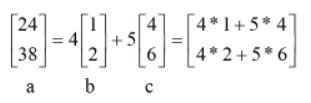
In the above example, 4b is a scalar multiple of b, and 5c is a scalar multiple of c. Hence, a is a linear combination of b and c.
Conclusion:
Following are the properties of Combinations; using these formulas, one can solve most problems related to the Combinations and linear vectors.
- nC0 = nCn = 1
- nC1 = nCn-1 = n
- nCr = nPr / r!
- nCr + nCr-1 = n+1Cr
- nCr = nCn-r
- r nCr-1 = (n-r+1) nCr-1
