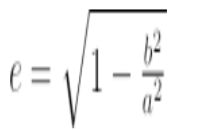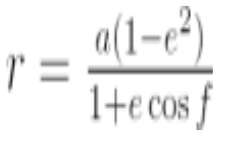One of the four classic conic sections generated by dissecting a cone with a plane is the ellipse. The parabola, circle, and hyperbola are the others. Celestial objects in periodic orbits around other celestial objects invariably trace out ellipses, which is why the ellipse is so significant in astronomy.
The locus of all locations in the plane for which the sum of the distances r1 and r2 to two fixed points F1 and F2 (called the foci) separated by a distance 2c is a constant 2a is called an ellipse.
As a result of this formulation, the elliptical equation is: r1+ r2 = 2a, where a = semi-major axis.
The most common way to write a Cartesian Equation of Ellipse coordinates, with the origin on the x-axis between the two foci.
The ellipse equation can be rewritten as: b2 = a2 – c2 if the semi-minor axis is defined as
where
a = axis of semi-majority
b = axis of semi-minority
The eccentricity of an ellipse describes its shape. The ellipse is considered to be eccentric if the semi-major axis is bigger than the semi-minor axis. Excessiveness is defined as:
Substituting b in the equation above yields another important relationship:
ae = c
The eccentricity is then defined as the distance between the foci as a proportion of the semi-major axis.
With the origin on one of the foci, polar coordinates, radial distance r, and angle f can be used to specify the position of a point on an ellipse.
The ellipse equation can also be expressed in terms of polar coordinates (r, f). When we replace x and y in the ellipse equation, we get:
The circle is a specific case of an ellipse with c = 0, in which the two foci coincide and the circle’s center is formed. If we substitute zero eccentricity for an in the equations above, we get a = b, which means that both axes are equal to each other and the radius of the circle.
The area of the ellipse formula is Area = Pi * A * B
How to Draw an Ellipse?
There are specific steps to drawing an ellipse in mathematics. The following is a step-by-step approach for drawing an ellipse with provided dimensions.
- Determine the length of the main axis, because the major axis is the ellipse’s longest diameter.
- Draw one horizontal line the length of the primary axis.
- Using a ruler, mark the midpoint. This can be accomplished by splitting the length of the principal axis by two.
- Using a compass, create a circle with this diameter.
- Determine the length of the minor axis, which is the ellipse’s shortest diameter.
- Take the protractor and fix its origin at the midpoint of the major axis. Mark the spot at 90 degrees. Then, using the protractor, swing it 180 degrees and mark the spot. The minor axis can now be drawn between or inside the two markings at its halfway point.
- Using a compass, draw a circle of this diameter, just as we did for the major axis.
- Divide the entire circle into twelve 30-degree segments using a compass. This can be accomplished by placing your protractor on the main axis at the origin and identifying the intervals of 30 degrees with dots. Then, using lines, connect the dots in the middle.
- From the inner circle, draw horizontal lines (save for the major and minor axes).
- They run parallel to the main axis and radiate outward from all sites where the inner circle and 30-degree lines converge.
- Make the lines a little shorter near the minor axis and a little longer as you go closer to the major axis.
- From the outer circle, draw vertical lines (save for the major and minor axes).
- They run parallel to the tiny axis, and they go inward from all sites where the outer circle and 30-degree lines converge.
- Draw the lines a little longer towards the minor axis, but a little shorter as you go closer to the major axis.
- If you see that the horizontal line is too far, you can lengthen the ruler a little before drawing the vertical line.
- Use your freehand drawing skills to draw the curves between the points.
Important Terms Related to an Ellipse
Let’s go through three key terms related to ellipses.
- Auxiliary Circle: The auxiliary circle is a circle drawn on the principal axis of the ellipse. The auxiliary circle to the ellipse has the equation x2 + y2 = a2.
- Director Circle: The director circle is the location of the points of intersection of the perpendicular tangents traced to the ellipse. The ellipse’s director circle has the equation x2 + y2 = a2 + b2
- Parametric Coordinates: (x, y) = (aCos, aSin) are the parametric coordinates of any point on the ellipse. These coordinates represent all points along the coordinate axes and satisfy all of the ellipse’s equations.
Conclusion
Here, we’ve learned the Cartesian Equation of Ellipse, how to draw an ellipse, and more!
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out