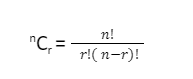Whenever you come across a complex binomial expression that has a big number as its exponent, you would be required to use the binomial theorem to expand it. If you go ahead and expand an expression line (x+z)345 all by yourself, it will take you an eternity. Whereas, using the binomial theorem, you can achieve the expanded number in a few minutes.
According to the binomial theorem, the total number of terms in the binomial expansion of a number cannot be more than n+1. And in every consecutive term, the exponent on the first term decreases, while the one on the second term increases from 0 to n.
Binomial Theorem Formula
According to the binomial theorem, every binomial expression can be expanded in different terms and the binomial expression is expressed as the sum of all of these terms. The theorem can be expressed in the form of a formula as
(p+q)^n = nC0p^n + nC1p^n-1q^1 + nC2p^n-2q^2 +………. + nCnp^n-rq^r +…… + nCnq^n
This is the binomial expansion of the term (p+q)n. And to find a term in this expanded form, you can use the formula of the general term in a binomial expansion.
For the expansion of (a+b)n, the general term will be ( T r+1)
so, T r+1 = nCnx^n-ry^r for r = 0, 1, 2……, n
One important thing to note here is that while finding the first term of the binomial expansion, you should not put 1 at the place of r because that will give you the 2nd number in the series. So, always use zero instead of one to find the first term in the given binomial expansion.
Binomial Theorem For Positive Index
When a binomial expression has a positive coefficient, the binomial theorem for positive index states that “ the total number of terms in the expansion is one more than the index”. For instance, in the expansion of (x + y)n, the total number of terms that can be obtained on its expansion is n+1. Whereas the index of (x + y)n is n, where n is the positive integer.
Using the binomial theorem, we can expand (x+y)n, where n can be a rational number. Let’s see the expansion of (x+y)n
(x+y)^0 = 1
(x+y)^1 = (x+y)
(x+y)^2 = x^2 + 2xy + y^2
(x+y)^3 = x^3 + 3x^2y + 3xy^2 + y^3
(x+y)^4 = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4
Properties Of Binomial Theorem For Positive Index
The Binomial theorem for the positive index has the following properties.
- When you see the power of each term in the binomial expansion, there is a pattern that you will come across. The exponent on the first term moves in descending order from n to 0, whereas the exponent of the other term increases with each term. Let’s understand it with an example
(a+b)^4 = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4
Here, you can see that the exponent decreases from 4 to 0 in each consecutive term. At the same time, the exponent of the term b increases from 0 to 4. This indicates that the given expression is a binomial expression.
- The total number of terms in a binomial expansion, according to the binomial theorem, is more than the value of the exponent on the binomial expression. For instance, the binomial expansion of (a+b)^4 is a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4. In this expression, the total number of terms is 5, which is one more than the positive index or exponent of the expression
- The sum of the exponents of both the terms in any expression will always be equal to the exponent of the binomial expression that is expanded. For example
(x+y)^3 = x^3 + 3x^2y + 3xy^2 + y^3
Here, the total value of the index is 3 and if you add the index of any term in the expression, you will find that the sum is equal to 3. Take 3xy2, for example. The sum of the index of x, i.e., 1 and the index of y, i.e., 2, is equal to 3. This proves that this equation is a binomial expression.
Properties Of Coefficients In Binomial Expansion Of Positive Index
Coefficients are those numbers that are associated with each term in a binomial expansion. Some of the important properties of coefficients are
- According to the binomial theorem, the coefficient of the first and last term is in a binomial expansion
- The Pascal triangle states that if the coefficients of a binomial expansion are arranged in a triangle, it can be arranged in a way that every number is equal to the sum of two numbers above it
- The coefficient of any of the terms in a binomial expansion can be obtained using the combination formula
Where r is any position of the term for which you want to find the value of the coefficient.
Binomial Theorem Calculator
A binomial theorem calculator is the one that is used to find the expanded form of binomial expressions. You need to put the expression in the search box with its coefficient, and you will obtain its expanded form in the result dialogue box.
Conclusion
The binomial theorem is often used in the calculation of complex mathematical questions. To calculate the binomial expansion of a binomial expression with a positive index, you need to apply the binomial theorem for positive index. This theorem has various postulates that we have discussed extensively in our discussion.
Moreover, you should also explore topics, such as how to find the value of middle-term and constant terms using the binomial theorem formula. Learn the concept of general terms in a binomial expansion to be able to find the exact term in a binomial expansion. Furthermore, find out more ways in which you can use a binomial theorem calculator efficiently.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out