Profile
Settings
Refer your friends
Sign out
Trigonometry, Trigono + Metry = Triangle + Measure. Trigonometry is used in many areas, such as designing electric circuits and analyzing musical tones. It is the science of measuring triangles by angles.
Practically, Trigonometry has innumerable uses. It is used in the study of earthquakes to help predict their intensity and location. It can even be used to calculate the height of tides! Trigonometry is a fascinating subject with many real-world applications.
Trigonometric functions were first introduced by Indian mathematicians in 432 AD. Although, they didn’t understand trigonometry as we do today. It wasn’t really developed until the 16th century. This was when European mathematicians started using algebra to solve trigonometric equations.
Trigonometry is a vital part of mathematics. Trigonometry formulae include sine, cosine, tangent, cosecant, secant, and cotangent. Trigonometry calculators can be used to find the value of a trigonometric function. They take inputs, i.e., the value of the angle in radians or degrees.
Degree and Radian Measure
When working with trigonometric functions, it is important to be able to convert between degrees and radians. A degree is a measure of the angle that is defined as 1360 of a circle. A radian is a measure of the angle that is defined as the angle subtended by an arc of length equal to the radius of the circle.
To convert from degrees to radians, multiply the degree measure by π/180. To convert from radians to degrees, divide the radian measure by π/180.
Here are some examples:
Convert 45 degrees to radians:
45*π/180=0.785398
Convert 0.785398 radians to degrees:
0.785398*180/π=45 degrees
Trigonometric Ratios (Acute Angle)
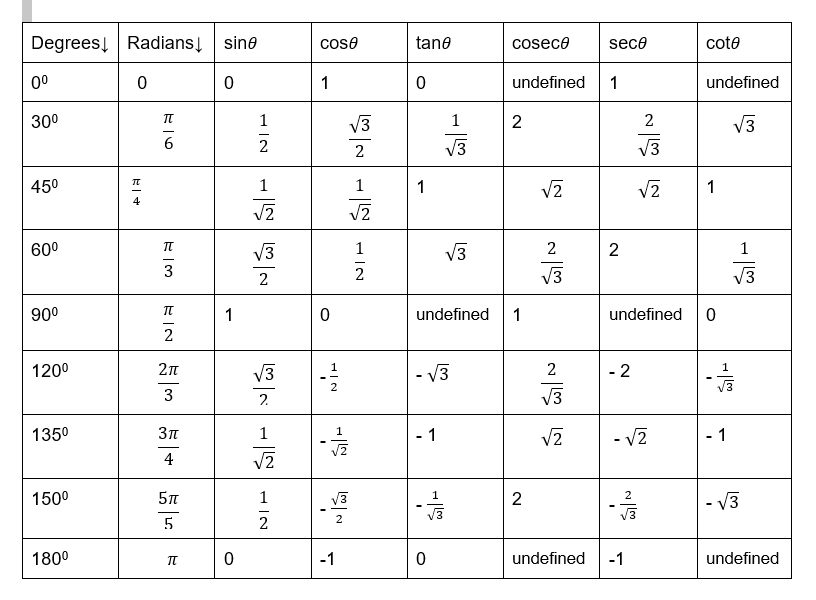
Trigonometric ratios are used to find the ratio of two sides in a right triangle. The value of trigonometric ratios is between -infinity to infinity.
The following table shows the trigonometric ratios for different angles(<=1800);
Trigonometric Functions (Any angle)
Trigonometric Functions are used in many real-world applications. They can be defined for any angle, but the most common angles that they are applied to are acute and obtuse angles. The more commonly known trigonometric functions include sine, cosine, tangent, secant & cosecant, which all have their own unique properties.
All of the trigonometric functions can be graphed on a unit circle. The point (x, y) where the function is equal to 0 is called the origin. The angle θ is measured in radians and increases as you go around the unit circle counterclockwise.
![]()
Sine Function
Sine FunctionThe sine function is used to find the ratio of the length of the opposite side to the length of the hypotenuse. The sine function is also used to calculate angles in radians and degrees. It has an amplitude of one and a period of 2π.
Cosine Function
The cosine function is used to find the ratio of the length of the adjacent side to the length of the hypotenuse. The cosine function is also used to calculate angles in radians and degrees. It has an amplitude of one and a period of 2π.
Tangent Function
The tangent function is used to find the ratio of the opposite side to the adjacent side. The tangent function is also used to calculate angles in radians and degrees. It has an amplitude of one and a period of π.
Secant Function
The secant function is reciprocal of the cosine function. The secant function is also used to calculate angles in radians and degrees. It has an amplitude of one and a period of 2π.
Cosecant Function
The cosecant function is reciprocal of the sine function. The cosecant function is also used to calculate angles in radians and degrees. It has an amplitude of one and a period of 2π.
Cotangent Function
The cotangent function is reciprocal of the tangent function.The tangent function is also used to calculate angles in radians and degrees. It has an amplitude of one and a period of π.
Domain and Range
The domain of a function is the set of all values for which the function produces a result. The domain of a trigonometric function is the set of all real numbers. The range is the set of all real numbers that the function can produce a result. The range of trigonometric functions depends on the function in consideration.
For example, the domain of sine is all real numbers because sin(π/12) = 0.984375 and sin(-π/12) = -0.984375, both of which are real numbers. The range of sine is all real numbers less than or equal to one because sin(x) can never be greater than or equal to one.
Principal and General Solution of a Trigonometric function
Principal solutions: The solutions where 0 ≤ x < 2π are known as principal solutions
General solution: The statement that integer ‘n’ gives all solutions to a trigonometric equation. To obtain a general solution, use the fact that the sine and cosine values repeat after an interval of 2π. The value of tan x repeats at π.
Note that
For any real numbers x and y, sin x = sin y implies x = nπ + (–1)ny, where n ∈ Z
For any real numbers x and y, cos x = cos y, implies x = 2nπ ± y, where n ∈ Z
If x and y are not odd multiples of π/2, then tan x = tan y implies x = nπ + y, where n ∈ Z
Conclusion
Trigonometric functions are used to find the ratios of lengths in right triangles. The six basic trigonometric functions have unique properties and can be graphed on a unit circle. The domain of the trigonometric functions is all real numbers, and their range depends on which function is being graphed. The inverse trigonometric functions can be used to solve for angles in radians or degrees.
