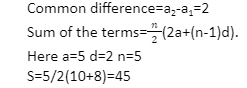Arithmetic Progression Examples

Arithmetic progression maintains a sequence or series of numbers with the same gaps or skips between alternative numbers, and the difference between them remains constant. Let’s look at an introductory example of arithmetic progression.

The sequence 7, 9, 11, 13, 15,… is an example of a progression with a standard difference of two. Let us understand the topic with examples.

Arithmetic Progression Examples

A finite progression, sometimes simply called progression, refers to a finite portion of a progression between numbers. An arithmetic series is the sum of a finite progression.

The formulas for arithmetic progression are demonstrated below.

The common difference of an arithmetic progression is d = a2 – a1.

The nth word of an arithmetic progression is a = a + (n – 1)d.

The total of an arithmetic progression’s n phrases is Sn = n/2 (2a+(n-1)d).

An arithmetic progression is a series in which differences between two subsequent words are equal, offering a chance to develop a formula for the nth term in a progression. For example, the sequence 3, 7, 11, 15,… is an arithmetic progression because it adheres to a pattern where each number is obtained by adding 4 to its preceding term. During this series, the nth term equals 4n-1. The sequence’s terms are frequently generated by inserting n=1,2,3,… within the nth term. i.e.,

When n = 1, 4n-1 = 4(1)-1 =3

When n = 2, 4n-1 = 4(2)-1 = 8-1= 7

When n = 3, 4n-1 = 4(3)-1 = 12-1=11

So, how do we calculate the nth term of a given sequence?

1. Find the sum of the series: 8 + 16 + 24 + 32 + 40 + 48 + ……….. + 256

Solution:

The first term of the given sequence of arithmetic series = 8

The second term of the given sequence of arithmetic series = 16

The third term of the given sequence of arithmetic series = 24

Therefore, Second term of sequence – First term of sequence = 16 – 8 = 8

Third term sequence of the series – Second term sequence of the series = 24 – 16 = 8

Hence, the given sequence of the series is an arithmetic series with the common difference 8.

Let there be n terms within the given arithmetic series. Then

an = 256

⇒ a + (n – 1)d = 256

⇒ 8 + (n – 1) × 8 = 256

⇒ 8 + 8n – 8 = 256

⇒ 8n  = 256

⇒ n = 32

Hence, the specified sum of the series = 

S = n/2 [2a +(n-1)d]

32/2[2 ∙ 8 + (32 – 1) ∙ 8]

= 16 [16 + 30 ∙ 8]

= 16 [14 + 240]

= 16 × 254

= 4064

2. Chris earns $200,000 once a year, and his salary increases by $10,000 once a year. Calculate the amount he earns in four years?

Solution: The amount earned by Chris for the first year is, a = 200,000. The increment d = 10,000. We need to calculate his earnings within the four years. So n = 4.

Substituting these values within the arithmetic progression sum formula,

Sn=n/2[2a+(n-1) d]

Sn= 4/2(2(200000)+(4-1)(10000))

= 2 (400000+30000)

= 2 (430000)

= 860000

He earned $ 860,000 in four years

3. Calculate the sum of the subsequent arithmetic series:

2 + 9 + 16 + 23 + 30 + 37 + ………………… to 14th terms

Step by step solution of the sum of the progression arithmetic series:

Common difference:

Second term – First term = 9 – 2 = 7

Third term – Second term = 16 – 9 = 7

Fourth term – Third term = 23 – 16 = 7

Therefore, the common difference of the given arithmetic series is 7.

The number of terms of the given A. P. series (n) = 14

The sum of arithmetic series is given by the formula:

S = n/2[2a + (n – 1)d]

= 14/2[2 ∙ 2 + (14 – 1) ∙ 7]

= 7 [4 + 13 ∙ 7]

= 7 [4 + 91]

= 7 × 95

= 665

4. Write the derivation of the sum of arithmetic progression.

We start with the first term and successively add on the common difference.

Sn = a1 + (a1 + d) + (a1 + 2d) + … + [a1 + (n–1)d].

We can also start with the nth term and successively subtract the common difference, so,

Sn = an + (an– d) + (an – 2d) + … + [an – (n–1)d].

Thus the sum of the arithmetic sequence could be calculated either way. However, after adding those two equations, we get

Sn = a1 + (a1 + d) + (a1+ 2d) + … + [a1 + (n–1)d]

Sn = an + (an – d) + (an – 2d) + … + [an – (n–1)d]

2Sn = (a1 + an) + (a1 + an) + (a1 + an) + … + [a1 + an].

Notice all the d terms are added out. So,

2Sn = n (a1 + an)

Sn = [n(a1 + an)]/2

By substituting an = a1 + (n – 1)d into the last formula, we have

Sn = n/2 [a1 + a1 + (n – 1)d] …Simplifying

Sn = n/2 [2a1 + (n – 1)d].

Both formulas help us quickly calculate the sum of an arithmetic series.

Conclusion

A finite progression, sometimes simply called progression, refers to a finite portion of a progression between numbers. An arithmetic series is the sum of a finite progression. Arithmetic progression maintains a sequence or series of numbers with the same gaps between alternative numbers, and the difference between them remains the same.