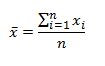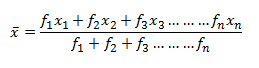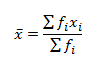Arithmetic Mean

Arithmetic Mean refers to the average of the values, which we can also understand as the sum of all values divided by the total number of values in a particular set. It is one of the most commonly used measures of central tendency employed to make a statistical summary of enormous data. A simple example to understand arithmetic mean is how the report card focuses on the aggregate marks to simplify the interpretation instead of stating the different marks one has scored in multiple subjects throughout the year. This central tendency is, thus, beneficial in interpreting large value sets to come to valuable conclusions. 

Arithmetic Mean in Statistics

To define arithmetic mean in statistics, we can say that it is the average of the data set provided. We can find it by dividing the sum of all the values in the data set by the total number of values. 

For n values in a particular data set namely x1, x2, x3, … xn, the mean can be found by:

x̄ = x1+ x2+ x3+ … +xn / n

We can also write the same formula as: 

A different formula is used for calculating the mean when the observation frequency is given. If x1, x2, x3,… xn are the recorded observations and f1, f2, f3 … fn are the respected frequencies of these observations, then the Mean is: 

We can also write the same formula as: 

These are the formulae used when calculating the mean of ungrouped data. For calculating the mean of grouped data, we must calculate the class mark. 

Class mark= (Upper Limit + Lower Limit) / 2

After we calculate the class mark, the mean can be calculated similarly using the above formula by replacing xi with the class mark.

Let us take an example to understand it better. 

Example 1: 

Find the mean value of the given set: 3, 4, 6, 7, 8

Mean = (3+4+6+7+8)/5 = 28/5=5.6

Example 2: 

Find the mean of the first five prime numbers. 

As we know, the first five prime numbers are 2, 3, 5, 7, and 11. 

Mean = (2+3+5+7+11)/5 = 28/5= 5.6

Arithmetic Mean Properties

Let us now look at some arithmetic mean properties to understand the concept better.

1. If all the numbers in a given set have the same value, k, then the arithmetic mean would also be k. For example: The mean of the five numbers 12, 12, 12, 12, and 12 will be (12+12+12+12+12)/5 = 12. 
2. The algebraic sum of the deviations of a given set from their arithmetic mean is always zero. It can be stated as (x1−x̄)+(x2−x̄)+(x3−x̄)+…+(xn−x̄) = 0. For ungrouped data, it can be written as ∑(xi−x̄) = 0, and for grouped data, it can be written as ∑fi(xi−x̄) = 0.
3. If each number in a set decreases or increases by the same value, the arithmetic mean would also decrease or increase by a similar value. Suppose the mean of a set is x1, x2, x3 ……xn is X̄, then x1+k, x2+k, x3 +k ……xn+k will also be X̄+k. 
4. If each number in a set gets multiplied or divided by the same value, then the arithmetic mean would also be multiplied or divided by a similar value. If the mean of a set  x1, x2, x3 ……xn is X̄, then x1/k, x2/k, x3/k ……xn/k will also be X̄/k. As for division, the fixed value must be a non-zero number since division by 0 does not give a defined number. 

Advantages of Arithmetic Mean 

The arithmetic mean is useful in statistics and mathematics and in economics, experimental science, sociology, and other similar disciplines. Here are some benefits of arithmetic mean: 

1. The formula for finding out the arithmetic mean is rigid and does not change based on the position of the value in any given set. Unlike median, mean is a more stable and rigid central tendency. 
2. Mean is constituted by considering every value present in any given set. 
3. The formula for calculating the mean is simple. Any person with basic addition and division skills can find out the arithmetic mean. 
4. Mean provides valuable results irrespective of the size of the data set. It helps in the interpretation of a large value set with ease. 
5. Mean can be used for further mathematical operations, unlike other algebraic expressions like mode and median. 
6. Mean also has applicability in geometry. For instance, the coordinates of the centroid of a triangle are also the arithmetic mean of the vertex coordinates. 

Disadvantages of Arithmetic Mean 

Along with advantages, there are also some disadvantages of arithmetic mean, such as:

1. One of the main disadvantages of arithmetic mean is that it gets affected by large values in the data set. For example, if the marks scored by different students in a particular exam are 10, 20, 30, 20, 30, and 90, the arithmetic mean is (10+20+30+20+30+90)/6 = 33.33 that is majorly affected by 90, an extreme value in the set. 
2. Mean value can solely be used for quantitative data and not qualitative data such as honesty, hard work, etc. 
3. Mean value cannot be calculated even if a single value is unknown since every value impacts the average. 
4. There is no means to locate the arithmetic mean, either graphically or through inspection. 
5. Arithmetic mean cannot be found out in the case of open-ended classes without making a rough assumption of the class size.