Profile
Settings
Refer your friends
Sign out
Angles are formed when two straight lines meet at a point. When two lines intersect, then four angles are formed. The angles that are aligned and have one common arm are known as adjacent angles. The angles that are not adjacent and do not have a common arm are known as vertically opposite angles. Let us learn about the types of angles between two intersecting lines and the adjacent and opposite angle theorems.
Adjacent Angle Theorem
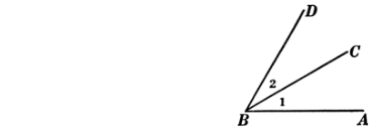
Adjacent angles are the ones that have one common arm and vertex. In this diagram, we can see that angle 1 and angle 2 are adjacent angles. They have a common arm as BC and vertex B.
The adjacent angle theorem states that the sum of adjacent angles on a straight line is equal to 180°.
The angle ∠BOD and ∠DOA are two adjacent angles on a straight line. According to the adjacent angles theorem, we will have:
∠BOD + ∠DOA = 180°
The example of adjacent angles in real life is that of pizza slices that are placed next to each other forming adjacent angles.
Opposite Angle Theorem
Opposite angles or vertically opposite angles are not adjacent to each other and are aligned oppositely.
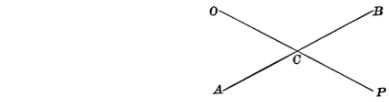
The angles ∠BCP and ∠ACO are vertically opposite angles. Similarly, ∠ACP and ∠BCO are said to be vertically opposite angles.
The opposite angle theorems state that the angles that are aligned oppositely are of equal measurement. Therefore we will have:
∠BCP = ∠ACO and ∠ACP = ∠BCO
Let us prove that the opposite angles are equal:
We have for the above figure:
∠BCP + ∠PCA = 180° (adjacent angles) (i)
∠PCA +∠ ACO= 180° (adjacent angles) (ii)
On subtracting equation (ii) from equation (i), we get:
∠BCP – ∠ACO = 0
Hence,
∠BCP = ∠ACO
Opposite Angle in Parallelogram
In a parallelogram, opposite angles are aligned oppositely to each other and have an equal measurement.
In this parallelogram, we have have ∠CBA = ∠ADC and ∠BCD = ∠DAB. They are opposite angles.
Example: The opposite angles of a parallelogram are (2x – 5) and (x – 3). Find the value of x?
Solution: The opposite angles of a parallelogram are equal. Therefore, we get:
2x-5=x-3
2x-x= -3+5
x=2
Example: The opposite angles of a parallelogram are (2×2 – 3) and (x – 3). Find the value of x?
Solution: The opposite angles of a parallelogram are equal. Therefore, we get:
2×2-3=x-3
2×2-x= -3+3
2×2-x=0
(2x-1)x=0
So we are getting 2 values of x which are x=½ and x=0
But by putting values of x in the above equations we will get
Putting x=0 ∠A =-3 and ∠B =-3 since angles can not be negative hence x=0 is rejected
Putting x=½ ∠A=-2.5 and ∠B=-2.5 since angles can not be negative hence x=0 is rejected
So there exists no such value of x for which angles are opposite.
Example: If one angle is 60°, find all the other angles of a parallelogram.
Solution: We are given that ∠A=60°. Then:
∠A+∠B= 180°(sum of Consecutive angles is 180)
∠B= 180°-∠ A
∠B= 180°-60°
∠B= 120°∠A=∠ C=60° (Opposite angles are always equal)
∠B=∠ D=120° (Opposite angles are always equal)
So we finally calculated all angles of a parallelogram
∠A=∠ C=60°
∠B=∠ D=120°
Difference Between Adjacent Angles and Opposite Angles
Adjacent Angles | Opposite Angles |
Adjacent angles have a common arm and a vertex. | Opposite angles do not have a common arm but have a common vertex. |
Adjacent angles may or may not be equal. | Vertically opposite angles are always equal. |
Adjacent angles are aligned next to each other. | Opposite angles are aligned oppositely. |
Some Important Notes
- The sum of two adjacent angles is formed by two non-common arms and one common arm.
- The adjacent angles whose sum is equal to 180 degrees are known as linear pairs.
- Vertically opposite angles can be both supplementary and complementary.
- Vertically opposite angles are non-adjacent.
Conclusion
The intersecting lines are those that cross each other at the point of intersection. When any two lines intersect, they make four angles. Adjacent angles are those that have the same arm and the vertex. They may or may not be equal. As per the adjacent angle theorem, the adjacent angles on a straight line have a sum equal to 180 degrees.
The angles that are aligned oppositely are known as vertically opposite angles. They are always equal to each other. That is why, in a parallelogram, vertically opposite angles are equal. So this was all about the types of angles between two intersecting lines and their theorems.
