Processes such as nerve transmission and membrane potentials can be studied using the Nernst equation.
A wide variety of thermodynamic and electrochemical properties, potentiometric titrations, and cell membrane resting potential calculations rely on electrochemical cells and, as a result, the Nernst equation.
Electrode potential and standard electrode potential are linked using Nernst’s equation.
It can also estimate the spontaneous nature of an electrochemical reaction and derive free energy from the Gibbs function.
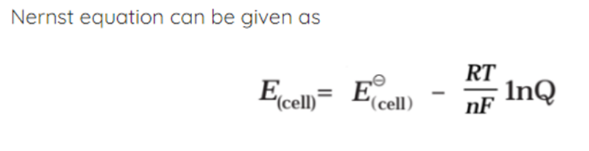
- E0 is the cell potential under normal circumstances.
- R is an abbreviation for the standard gas constant.
- T is Temp.
- N is the number of electrons that are exchanged in the redox reaction.
- F is Faraday’s constant
- Q denotes the quotient of reactions.
Key Aspects Related to the Nernst Equation:
Electrochemical cell potential can be calculated using the Nernst equation at any specified temperature, pressure, or concentration. The reduction potential of the cell in a non-standard situation is connected to the cell’s reduction potential under standard conditions via this equation (298K, 1 atm, and 1 M concentration).
The standard electrochemical potential is the voltage difference between a redox reaction under normal conditions (1 molar for aqueous solutions, 1 atmosphere for gases). For gaseous or liquid reactants, the voltage is also affected by the concentration or pressure of the reactants because the average energy of the components changes with concentration or pressure. Under 1 M solution and 1 atm gas conditions, the Nernst equation determines the voltage.
This equation can be used to compute half-cell reactions and cell potentials for different electrochemical cells. The term RT/nF is simplified to a constant in various other equation versions. For example, the natural log can be changed to log to make the equation more similar to the pH equation.
When the concentration of a reactant is increased, the Nernst equation can determine the rise in cell potential. There will be no difference in cellular potential when Q equals 1. The conventional cell potential will deviate if Q is changed in any way. The cell potential will be lower if the Q value is greater than 1. A Q value of less than 1 indicates that the standard will be exceeded.
Limitations in Using the Nernst’s Equation:
Although Nernst’s equation has few constraints, some assumptions are required when using the equation. This equation can be incorrect in various situations, some of which are shown below.
- Using the Nernst equation in high concentrations leads to incorrect results. Experiments determine potentials when reactant or product concentrations are exceedingly high.
- Dilute solutions have a theoretical capacity for infinite potential, which should be disregarded because it is unrealistic.
- When current flows through the cell, the equation cannot be employed. The current alters the ions’ activity (effective concentration). As a result of this, the equation turns out to be wrong.
Important Facts:
- The equation was derived by Walther Hermann Nernst, a German chemist, in 1864.
- In recognition of his contributions to thermochemistry, Nernst was awarded the 1920 Nobel Prize in Chemistry.
- The third law of thermodynamics, also made by Nernst, is well-known.
- The Nernst equation has several applications in electrochemical cell potentials. Most batteries use electrochemical cells as their power source. These cells can also coat other surfaces, such as jewellery, with tiny compound layers.
Gibbs energy of reaction:
Using the Gibbs free energy (also known as Gibbs energy) of a thermodynamic system at a constant temperature and pressure, it is possible to compute the maximum reversible work that can be performed.
A thermodynamically closed system’s maximum non-expansion work is represented by its Gibbs free energy (which can exchange heat and work with its surroundings). The entire procedure must be reversible to reach this limit. During reversible transitions between initial and final states, the Gibbs free energy is reduced by the amount of work a system does about its surroundings, minus any work performed by pressure forces.
When a system achieves chemical equilibrium at constant pressure and temperature, the thermodynamic potential known as the Gibbs energy is minimised. For the reaction coordinate, its derivative disappears at an equilibrium point in the system. G must be reduced to allow spontaneous reactions to occur at any pressure or temperature.
The amount of “free” or “useful” energy available to accomplish work can be equated to G. The equation can also be seen from the perspective of the system as a whole (the rest of the universe).
To begin with, one assumes that the specified reaction at constant temperature and pressure is the only one taking place at this time and place. The entropy released or absorbed by a system equals entropy that the environment has to absorb or release. Entropy change in the cosmos must be zero or positive for the reaction to be allowed. An exergonic reaction has a negative G, which may be seen in the reaction’s results.
Conclusion
This Nernst equation can be used to compute half-cell reactions as well as cell potentials for different electrochemical cells. The term RT/nF is simplified to a constant in various other versions of the equation. The natural log can be changed to log to make the equation more similar to the pH equation. The amount of “free” or “useful” energy available to accomplish work can be equated to G. The equation can also be seen from the perspective of the system as a whole (the rest of the universe).
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






