What are Special Parallelograms and their Importance in Mensuration

In the subject of geometry, the shapes can be separated into two distinct groups, which are as follows:

• Two dimensional
• Three dimensional 

Two-dimensional shapes, also known as flat shapes, are forms that only have two dimensions, such as length and breadth, in their representation. It is very thin and has no thickness. The square, the rectangle, the triangle, and other similar figures are all instances of 2D shapes.

Solids are another name for three-dimensional shapes because they have three dimensions including length, breadth, and width. Three-dimensional shapes are also known as three-dimensional shapes. It is possible to create three-dimensional objects by rotating flat shapes. Each of the solids’ faces has to have a two-dimensional shape. The sphere, the cuboid, the cone, the cylinder, and so on are all instances of three-dimensional shapes. 

Parallelogram: 

A quadrilateral that has two pairs of sides that are parallel to one another is called a parallelogram. Both of the opposing sides are parallel to one another and are the same length. Measure-wise, the diagonal angles are equivalent to one another. It has two diagonals that cross each other in the middle and the adjacent angles add up to a total of 360 degrees. In this piece, we will talk about three distinct types of parallelograms: the rhombus, the rectangle, and the square. 

Properties of parallelogram: 

A unique kind of polygon known as a parallelogram is formed when a quadrilateral has a pair of parallel opposite sides. The following is a list of the characteristics of a parallelogram:

1. The opposite sides are parallel and congruent
2. The angles on opposite sides are identical.
3. The angles that follow one another are complementary.
4. In the event that even one of the angles is a right angle, then the remaining angles will also be right angles.
5. Both diagonals meet and cut each other in half.
6. Each diagonal cuts the parallelogram in half, creating two triangles that are congruent with one another.
7. The parallelogram has a property where the sum of the squares of all of its sides is equal to the sum of the squares of its diagonals. It is also known as the law of the parallelogram. 

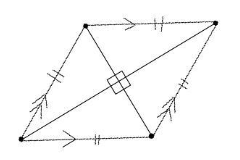
Rhombus: 

A quadrilateral in which all four of the sides are the same length is referred to as a rhombus. 

Properties of Rhombus: 

1. A rhombus has opposite sides that are parallel to one another and are of equal length. As a result, we have a parallelogram here.
2. A rhombus, on the other hand, has four sides that are each the same length.
3. Opposite angles are equal.
4. A rhombus has sides that meet at 90 degree angles, creating intersections at each corner.
5. The intersection of two diagonals creates a cross.
6. Diagonals cut through opposite vertex angles in a triangle.
7. Each of the diagonals cuts the rhombus into two triangles that are identical to one another. 

Rhombus formula: 

If the side is denoted by “a,” and the diagonals of the rhombus are denoted by “p” and “q,” respectively, then the formulas for calculating the area and perimeter of the rhombus are as follows: 

• Area of Rhombus = pq/2 Square units.
• Perimeter of Rhombus = 4a units

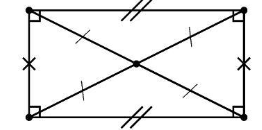
Rectangle: 

A parallelogram in which all four of the parallelogram’s angles have the same measure is called a rectangle. 

Properties of rectangle: 

1. Both of the opposing sides are the same length.
2. The opposite sides are parallel.
3. Every one of the inside angles is a perfect 90 degrees.
4. The length of each diagonal is the same.
5. The intersection of two diagonals creates a cross.

6.Each of the diagonals cuts the rectangle into two triangles that are identical to one another.

7. A horizontal and a vertical line of symmetry are present in its structure.

8. When linked in order, the four midpoints of the sides of a rectangle can be joined together to form a rhombus. 

Rectangle formula: 

The formula for calculating the area and the perimeter of a rectangle is as follows, with “l” and “b” standing for the length and width of the rectangles, respectively: 

• Area of Rectangle = lb square units
• The Perimeter of Rectangle = 2 (l+b) units. 

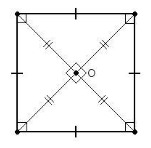
Square: 

A rectangle with four equal sides is called a square. 

Properties of square: 

1. The lengths of each of the four sides are identical.
2. The opposite sides are parallel.
3. Every one of the inside angles is a perfect 90 degrees.
4. The length of each diagonal is the same.
5. Each diagonal cuts the other diagonal across at right angles.
6. Diagonals cut through opposite vertex angles in a triangle.
7. It is a highly symmetric figure with 4 lines of symmetry, one horizontal, one vertical, and the two diagonals. These lines are arranged in a diamond shape.
8. Every one of the diagonals cuts the square into two triangles that are identical to each other. In point of fact, each of the two sets of triangles that are congruent to one another are likewise congruent to one another. 

Square formula: 

If “a” is one of the sides of a square, then the formula for calculating the area and the perimeter of a square is as follows: 

• Area of square = a² square units
• The Perimeter of the square = 4a units.

Conclusion: 

A parallelogram has four sides that are perpendicular to one another. Every one of the two sets of opposing sides has the same length and is aligned parallel to one another. The parallelogram, with its singular set of features, has found widespread use in industrial settings for the purpose of correctly transmitting mechanical motion from one location to another.