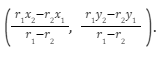A circle, in particular, is a closed curve that splits the plane into two regions: interior and exterior. In ordinary usage, the phrase “circle” can refer to either the figure’s boundary or the entire figure, including its inside; in strict technical terms, the circle is merely the boundary, and the entire figure is referred to as a disc.
A circle is also a special type of ellipse in which the two foci are coincident, the eccentricity is 0, and the semi-major and semi-minor axes are equal; or the two-dimensional shape enclosing the maximum area per unit perimeter squared, using calculus of variations.
Types of circles
- Concentric circles: Circles with the same centre are known as concentric circles. An annulus is the area between two concentric circles with different radii. By picking the inversion centre as one of the limiting points, inversion can be utilised to make any two circles concentric.
- Contact of circles: If two circles with centres C1x1y1 and C2(x2y2) and radii r1 and r2 respectively, touch each other externally, C1C2=r1+r2. Coordinates of the point of contact are A=
![]()
The circles touch each other internally if, C1C2=r1–r2. Coordinates of the point of contact are T=
3. Orthogonal circles: When two circles are sliced orthogonally, they form orthogonal curves and are referred to as orthogonal circles. A circle that is orthogonal to another circle has a 90-degree angle between them. The circles are considered to be orthogonal when this criterion is met. As a result, they are also known as perpendicular circles. Under inversion, orthogonal circles are invariant. Problem of Plane Strain in Plasticity is one of the many applications of orthogonal circles. S1=0 and S2=0 is given by S1+λS2=0, Where λ≠-1.
Circle family
1. Family of circles having a fixed centre
The equation is given by x-h²+y-k²=r²
Here (h,k) is fixed and r is a varying parameter. This is the equation of the family of concentric circles.
2. Family of circles passing through the point of intersection of line and circle
The equation for the circle S=0 family going through the point of intersection and line L=0 is given by S+λL=0,
Where is a parameter.
3. Family of circles passing through the point of intersection of two circle
S1+λS2=0, Where λ≠-1, is the equation of the family of circles passing through the point of intersection of two circles S1=0 and S2=0
4. Family of circles passing through two given points
The equation of the family of circles passing through two given points P(x1,y1) and Q(x2,y2) is given by
(x-x1)(x-x2)+(y-y1)(y-y2)+ λx y1 x1y2 1 x2 y2 1 =0
5. Family of circles touching a line at a given point
- The family of circles touching the line y-y1=mx-x1 at a point (x1,y1)
on any finite m has the equation(x-x1)²+(y-y1)²+λy-y1-m(x-x1)=0
If m is infinite, the equation becomes (x-x1)2+(y-y1)²+λx-x1=0.
Chord of two circles
Chord: The chord of the circle is a line segment that connects two places on the circle’s circumference. One of the line segments that can be drawn in a circle that has its endpoints on the circumference is the chord. To find the chord PQ, look at the circle below. A chord that goes through the centre of the circle is also known as a diameter.
Properties of the chord of a circle: A few key properties of a circle’s chords are listed below.
- The chord is bisected by a perpendicular drawn from the centre of the circle.
- The chords of a circle that are equidistant from the circle’s centre are equal.
- There is only one circle that travels through three intersecting points.
- When a circle chord is drawn, it divides the circle into two sections, which are referred to as the major and minor segments of the circle.
- A secant is formed when a chord is prolonged indefinitely on both sides.
Common Chord of two circles: We can connect the two crossing sites to form a common chord when two circles intersect.
The connecting line will be a perpendicular bisector of the common chord if we link the centres of these two circles.
At locations A and B, the circles O and Q intersect. Demonstrate that the line OQ connecting the two circles’ centres bisects AB and is perpendicular to it.
Conclusion
A circle is a planar shape formed by a closed curve with each point on the curve being the same distance from the circle’s centre. Everyone uses the concept of circles in geometry on a daily basis. It’s employed in agriculture, education, and architecture.
| Radius | The length between the centre and the edge. |
| Diameter | It begins on one side of the circle, travels through the middle, and then returns to the opposite side. |
| Circumference | The circumference of the circle’s edge. |
| Chord | A line that runs around the circumference of the circle from one point to another. |
| Tangent | As it goes past, the line “just brushes” the circle. |
| Arc | A section of the equator. |
| Sector | The portion of a circle that is limited by two radii and the circumference that lies between them. |
| segment | The distance between any two points on a line or curve, or the area of a solid sliced by a plane. |
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out