Profile
Settings
Refer your friends
Sign out
Surds are square roots of numbers that can’t be reduced to a whole number (W) or a rational number (Z) and can’t be represented accurately in a fraction. Surds are square root representations of irrational integers that cannot be stated in fractional or repeating decimals, in other words. Surds are utilized to perform exact computations. Let √3≈1.7320508, it is correct even more when it is √3 as a surd.
Surds Questions and Answers
Before facing the problems related to surds we must recap about the six rules of surds,
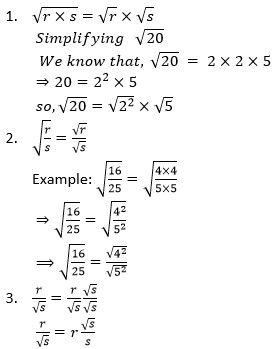
By multiplying the numerator and denominator with the denominator’s value, the denomination can be justified.
p√r ± q√r = (p+q)√r
Example: 5√2 – 3√2
= √2(5 – 3)
= 2√2
This rule essentially aids in the rationalization of the denominator. You must multiply p – q√r with both the numerator and the denominator.
This rule essentially aids in the rationalization of the denominator. You must multiply p + q√r with both the numerator and the denominator.
Let’s see some problems to test yourself
Questions
(i) √5 × √10
(ii) √8 × √6
(iii) √27 × √3
(iv) √16 × √4
(v) 5√8 × 2√6
(vi) √125 × √5
(vii) √100 × √2
(viii) 6√2 × 9√3
Answers:
(I) √5 × √10
= √5⋅10
= √5⋅5⋅2
= 5√2, which is an irrational number. Hence, it is a surd.
(ii) √8 × √6
= √8⋅6
= √2⋅2⋅2⋅2⋅3
= 4√3, which is an irrational number. Hence, it is a surd.
(iii) √27 × √3
= √27⋅3
= √3⋅3⋅3⋅3
= 3 × 3
= 9, which is a rational number. Hence, it is not a surd.
(iv) √16 × √4
= √16⋅4
= √2⋅2⋅2⋅2⋅2⋅2
= 2 × 2 × 2
= 8, which is a rational number. Hence, it is not a surd.
(v) 5√8 × 2√6
= √5 × 2 √2⋅2⋅2⋅2⋅3
= 10 × 2 × 2 × √3
= 40√3, which is an irrational number. Hence, it is a surd.
(vi) √125 × √5
= √125⋅5
= √5⋅5⋅5⋅5
= 5 × 5
= 25, which is a rational number. Hence, it is not a surd.
(vii) √100 × √2
= √100⋅2
= √2⋅2⋅5⋅5⋅2
= 2 × 5 × √2
= 10√2, which is an irrational number. Hence, it is a surd.
(viii) 6√2 × 9√3
= 6 × 9 √2⋅3
= 54 × √6
= 54√6, which is an irrational number. Hence, it is a surd.
Now, you have some idea about how to solve the problems. Here’s some practice problems for you champs.
Surds Practice Problems
Solved examples of Surds related questions
Example 1: 163/2 + 16-3/2 = ?
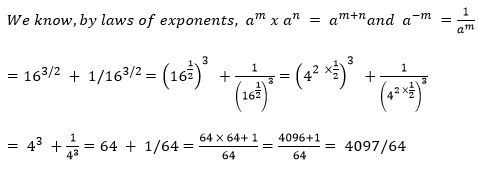
Example: If m and n are whole numbers and mn = 196, what is the value of (m – 3)n+1 ?
mn = 196
We know that 142 = 196
Hence we can take m = 14 and n = 2
(m – 3)n+1 = (14 – 3)2+1 = 113 = 1331
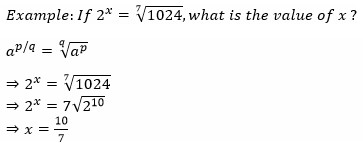
Example: Expand (2√2- √6)(2√2+√6), expressing the result in the simplest form of surd:
(2√2 – √6)(2√2 + √6)
= (2√2)2 – (√6)2, [Since, (x + y)(x – y) = x2 – y2]
= 8 – 6
= 2
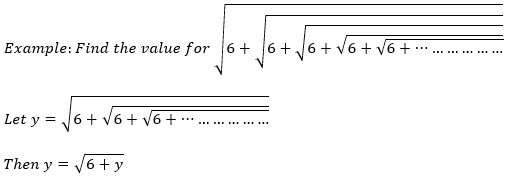
y2 = 6 + y
y2 – y – 6 = y – 3y + 2 = 0
y=3
Conclusion
When solving equations involving surds, we normally have to square them; however, when we square them, the domain of the equation expands, and we may receive some extraneous solutions; therefore, we must verify the solutions and disregard those that do not satisfy the equation.
It’s worth noting that assuming a = b from ax = bx is incorrect. x (a – b) =0, i.e., x = 0 or a = b, is the proper technique. Verification is required in this case.
