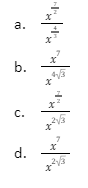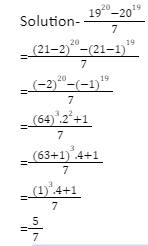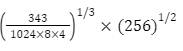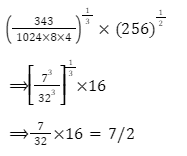Solve Indices Related Problems for CAT

Indices are used to display how many times a number has been multiplied by itself. They can also be used to represent roots and fractions, such as the square root. The principles of indices make it possible to alter expressions involving powers more quickly than if they were written out whole.

We’ll start with the formal notation for writing a number with an index, then go on to the laws that govern it. The number that appears on top of a number or letter is known as the index or power in mathematics. Indexes is the plural form of index. The number of times a number or character has been multiplied by itself is represented by an index.

Indices for CAT

Before we begin working with indexes, there are a few essential rules or laws that must be understood. These rules are applied while conducting algebraic operations on indices and solving algebraic equations, which includes it.

1. If the index of a constant or variable is ‘0,’ the outcome will be one, regardless of the base value.>X⁰=1 for any value of x
2. If the index has a negative value, the reciprocal of the positive index raised to the same variable might be used.>X^-r= 1 / X^r
3. We must sum the powers of two variables with the same base and raise them to that base to multiply them.>X^r.X^s=X^r+s
4. To divide two variables with the same base, subtract the denominator’s power from numerator’s power and raise it to that base.>X^r/ X^s=X^r-s
5. When a variable with one index is raised with another index, both indices are multiplied together and raised to the same base power.>Xrs=X^rs
6. When two variables with different bases but the same indices are multiplied, the base must be multiplied and the same index must be raised to the multiplied variables.>X^r.Y^r=XY^r
7. When two variables with different bases but the same indices are divided, the bases must be divided and the same index must be raised.>X^{r /} Y^r=XY^r
8. The radical form can be used to indicate an index in the form of a fraction.>X ^{r /s}=s √X^r

Some strategies and tips for CAT Indices preparation are included below.

1. Make a list of all the key formulas.
2. Fill out an application for all of the questions that are linked to it.
3. Understand the value and read the question carefully before calculating.
4. Practice all of the questions from last year’s exam.
5. Make as many mock tests as you can.

List of questions and answers for CAT

Here we have some problems with indices. Try and solve them.

1. If 2^2x+4 – 17 × 2^x+1 = –4, then which of the following is true?

A. x is a positive value

B. x is a negative value

C. x can be either a positive value or a negative value

D. None of these

Answer- C

2. If 3^{3+ 6 + 9 + ……… 3x}  = 0.037^-66, what is the value of x?

A. 3

B. 6

C. 7

D. 11

Answer-D

3. 4 ^{6+12+18+24+…+6x} = (0.0625)^-84, what is the value of x?

A. 7

B. 6

C. 9

D. 12

Answer- A

4. If a,b,c are non-zero and 14^a = 36^b = 84^c, then 6b(1 / c -1 / a) is equal to

A. 5

B. 3

C. 4

D. 99

Answer- B

5. If x=4096^7+4√3, then which of the following equals 64?

Answer- C

Solved questions of indices for CAT exams

1. If x²+x+1=0, then x²⁰¹⁸+x²⁰¹⁹ then equals which of the following

Solution-We know that,

 x³ – 1 = (x – 1)(x² + x + 1)

 Since, x²  + x + 1 = 0

 ∴ x³ – 1 = 0

  x³ = 1

 Now, x²⁰¹⁸ + x²⁰¹⁹

 = (x³)⁶⁷²* x² (x³)⁶⁷³

 = 1⁶⁷²* x² + 1⁶⁷³

 = x² + 1

 = -x

2. What is the remainder if 19²⁰ – 20¹⁹ is divided by 7?

3. If 9^{2x – 1} – 81^x-1 = 1944, then x is

Solution- We have to find the value of x

 ⟹ 9^{2x – 1}– 81^x-1 = 1944

 ⟹ 9^{2x – 1} – 92^x-1 = 1944

 ⟹ 9^{2x – 1} – 92^{x – 2} = 1944

 ⟹ (9^{2x – 2} × 9) – 9^{2x – 2} = 1944

 ⟹ 9^{2x – 2}  × (9 – 1) = 1944

 ⟹ 9^{2x – 2} =1944 / 8 = 243

 We can write 243 = 3⁵ = 9 5 / 2

 Comparing the powers,

 ⟹ 2x – 2 = 5/2

 ⟹ 2x = 9/2

 ⟹ x = 9/4

4. Given that x²⁰¹⁸ y²⁰¹⁷ = 1/2 and x²⁰¹⁶ y²⁰¹⁹ = 8, the value of x² + y³ is

Solution- x²⁰¹⁸ y²⁰¹⁷ =1 / 2 —(1)

x²⁰¹⁶ y²⁰¹⁹ = 8 —(2)

 Divide 1by 2we get (x / y)² =1 / 16

 y = 4x

 Substituting the value of y in (2)

 x²⁰¹⁶ . x²⁰¹⁹. 4²⁰¹⁹ = 2³

 x⁴⁰³⁵ . 2⁴⁰³⁸ = 2³

 x⁴⁰³⁵ = 2^-4035 => x =1 / 2 y = 2

 x² + y³ =33 / 4

5. If 5^x – 3^y = 13438 and 5^x-1 + 3^y+1 = 9686 , then x+y equals

Solution- It is given that5^x – 3^y = 13438 and 5^x-1 + 3^y+1 = 9686

 Let 5^x-1 = k and 3^y = m

 So, 5k – m = 13538 —- (1)

 k + 3m = 9686 —- (2)

 Multiply (1) by 3,

 15k – 3m = 40314 —-(3)

 Adding (2) and (3) we get,

 16k = 50000

 k = 625 x 5

 k = 5⁵

 We know, 5x-1 = k

 So, ^x-1 = 5

 x = 6

 We know, k + 3m = 9686

 3125 + 3m = 9686

 3m = 6561

  m = 2187

  m = 37 = 3^y

 y = 7  

 x + y = 6 + 7 = 13

Conclusion

In mathematics, indices are a useful tool for denoting the process of raising or lowering a number to a power or root. Taking a power is just the process of multiplying a number by itself several times, whereas taking a root is the same as taking a fractional power of the number. You can construct a single measure of change for a large number of objects by estimating index numbers. The formulas also demonstrate that the index numbers must be deciphered cautiously. The products that must be included, as well as the selection of a base period important.