Simple Method to find the Diagonal of Square

A square’s diagonal is a line segment connecting any two non-adjacent vertices. Two equal-length diagonals bisect each other at right angles in a square. When the side length of a square is known, the diagonal of the square formula is used to compute the length of the diagonal. 

Definition:

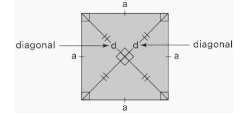
A square has two diagonals, each of which is produced by linking the square’s opposite vertices. Examine the following square to see how it relates to the diagonal qualities listed below.

• A square’s diagonals are all the same length.
• They are each other’s perpendicular bisectors.
• They divide the square into two isosceles right-angled triangles that are congruent.

Definition of square:

The square is a regular quadrilateral with equal length sides and angles on all four sides. The angles of the square are right angles, or 90 degrees. In addition, the square’s diagonals are equal and bisect each other at 90 degrees.

A square is a rectangle having two opposing sides that are both the same length.

The picture above depicts a square with all sides equal and all angles equaling 90 degrees.

A rhombus (which is also a convex quadrilateral with all four sides equal) can be considered a square if it has a right vertex angle, just like a rectangle.

A parallelogram with all two adjacent equal sides and one right vertex angle is a square in the same way.

Properties of a Square:

The following are the most essential square properties:

• The inner angles are all 90 degrees.
• The square’s four sides are congruent or equal in length.
• The square’s opposite sides are parallel to each other.
• The square’s diagonals intersect at 90 degrees.
• The lengths of the square’s two diagonals are equal.
• There are four sides and four vertices to the square.
• The square is divided into two identical isosceles triangles by its diagonal.
• The length of the diagonals is longer than the square’s sides.

Formula for diagonal of a square:

The formula for the diagonal of a square is d = a√2, where’d’ is the diagonal and ‘a’ is the square’s side. The Pythagoras theorem is used to find the formula for a square’s diagonal. A diagonal divides a square into two right-angled triangles that are isosceles. Both diagonals are congruent and cut each other in half at right angles. Let’s look at how to get the formula for finding a square’s diagonal.

Derivation of Diagonal of Square Formula:

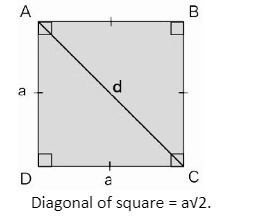
The length of both diagonals of a square is the same. The Pythagoras theorem is used to calculate the length of a diagonal, ‘d’, of a square of side length ‘a’. In the following square, the diagonal length is signified by the letter ‘d,’ while the side length is denoted by the letter ‘a.’

Consider the ADC triangle in the square. Because all of the angles of a square are 90 degrees, we can apply the Pythagoras theorem to get the hypotenuse, which in this case is ‘d’.      

 D² = a² + a²

d = √(a² + a²)

d = √(2a²)

d = √2 × √a²

= √2a

As a result, the square diagonal formula is d = a√2.

Importance of diagonal of square:

A square’s diagonal is a line segment that links two opposed vertices. We can have two diagonals within a square because there are four vertices. The diagonals of a square are always greater than the sides.

Area of Square Formula With Diagonal:

The diagonals of a square can be used to calculate its area. Along with the standard approach of squaring the sides to obtain the area of a square, there is another very helpful method of finding the area of a square using the length of a diagonal. ½ d² square units equal square area. The diagonal length is represented by d.

A square can be divided in the form of two right-angled triangles by drawing a diagonal from the vertices A to C, say the diagonal is of length ‘d’ units, as shown in the above diagram. Consider any right-angled triangle and use the Pythagoras theorem to solve it. According to Pythagoras’ theorem, we can write Hypotenuse² = Perpendicular² + Base² for every right-angled triangle. Perpendicular and Base will be ‘a’, and Hypotenuse will be ‘d’, because all the sides of a square are equal.

d² = x² + x²

d² = 2x²

x² = ½ d².

So, using the diagonal formula, the area of a square equals ½ d² square units.

Easy way to calculate the diagonal of a square:

1.  the length of one of the square’s sides. This is likely to be handed to you. If you’re dealing with a square in the real world, measure the length with a ruler or measuring tape. You can utilize any side of the square because all four sides are the same length. You can’t use this procedure if you don’t know the length of one of the square’s sides.
2. Create the d=s√2 formula. In the formula, one side of the square equals the length of the diagonal.

The Pythagorean Theorem (a² + b² = c²) is the source of this formula. Because a diagonal divides a square into two congruent right triangles, the length of the diagonal may be calculated using the square’s side lengths (which would be the hypotenuse of the right triangle).

3. In the formula, enter the square’s side length. Make sure the variable s is being substituted for.

4. Divide the length of the side by √2. This will give you the diagonal’s length. To achieve a more precise result, run the computation using a calculator. You can round √2 to 1.414 if you don’t have a calculator.

Conclusion:

The diagonals of a square are equal and intersect at 90 degrees. A square’s diagonal bisects its internal angle, generating adjacent 45° angles. 90° internal angle (degrees).