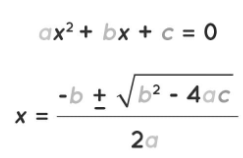Quadratic Equations

Quadratic equations have the form ax² + bx + c = 0 and are second-degree algebraic expressions. The term “quadratic” comes from the word “quad,” which means “square.” A quadratic equation is a “equation of degree 2,” in other words. A quadratic equation is employed in a variety of situations. Did you know that a rocket’s route is described by a quadratic equation when it is launched? A quadratic equation can also be used in physics, engineering, astronomy, and other fields.

Quadratic equations are second-degree equations in x with no more than two solutions. These two answers for x are known as the roots of quadratic equations and are denoted by the letters (,). In the next content, we will study more about the roots of a quadratic equation.

What is the definition of a quadratic equation?

A quadratic equation is a second-degree algebraic equation in x. The conventional form of the quadratic equation is ax² + bx + c = 0, with a and b as coefficients, x as the variable, and c as the constant component. The coefficient of x² is a non-zero term(α, β).

which is the first criterion for an equation to be a quadratic equation. The ² term is written first, followed by the x term, and finally the constant term when expressing a quadratic equation in standard form. Integral values, rather than fractions or decimals, are commonly used to express the numeric values of a, b, and c.

Formula for a Quadratic Equation

The most easy way for calculating the roots of a quadratic equation is to use the Quadratic Formula. Some quadratic equations are difficult to factor, and we can use this quadratic formula to acquire the roots as rapidly as possible in these circumstances. The roots of the quadratic equation can also be used to find the sum of the roots and the product of the roots. The quadratic formula’s two roots are written as a single equation. The equation’s two distinct roots can be obtained using either the positive or negative sign.

Quadratic Formula: The roots of a quadratic equation ax² + bx + c = 0 are given by x = [-b ± √(b² – 4ac)]/2a.

Methods to Solve Quadratic Equations

Two x values, or the problem’s two roots, can be obtained by solving a quadratic equation. One of four methods can be used to get the roots of the quadratic equation. The four methods for solving quadratic equations are as follows.

• Quadratic Equation Factorization
• Finding Roots Using a Formula
• Square Completion Techniques
• Finding the Roots Using Graphing

Let’s take a closer look at each of the methods listed above to see how to use them, as well as their applications and purposes.

Tips and Tricks for Solving Quadratic Equations

Some of the quadratic equations strategies and methods provided below will assist you in solving quadratic equations faster.

• Factorization is commonly used to solve quadratic problems. The formula is used when factorization fails to solve the problem
• The roots of a quadratic equation are sometimes known as the equation’s zeroes
• The roots of quadratic equations with negative discriminant values are represented by complex numbers
• A quadratic equation’s sum and product of roots can be used to find higher algebraic expressions involving these roots

Solved examples of Quadratic equations

Let’s try some additional problems this way.

Solve for x in Problem 1:  x²-3x-10 = 0.

Solution:

Let’s write -3x as the product of -5x and +2x.

x2-5x+2x-10 = 0 x2-5x+2x-10 = 0 x2-5x+2x-10 =

0 = x(x-5)+2(x-5)

0 = (x-5)(x+2)

x-5 = 0 or x+2 = 0 

x = 5 or x = -2 is the answer.

Problem 2: Find the value of x: x²-18x+45 = 0

Solution:

-15 and -3 are two numbers that add up to -18 and multiply to create +45.

By rewriting the formula,

x23. Using factorisation, find the roots of the equation 2×2 – 5x + 3 = 0.

Solution: Provided,

0 = 2×2 – 5x + 3

0 = 2×2 – 2x-3x+3

0 = 2x(x-1)-3(x-1)

(x-1) = 0 (2x-3)

So,

x = 3/2; 2x-3 = 0

x=1; (x-1) = 0

As a result, the roots of the above equation are 3/2 and 1.

Problem 3: Using factorisation, solve the quadratic equation 2x²+ x – 300 = 0.

2x²+ x – 300 = 0 is the solution.

0 = 2x² – 24x + 25x – 300

0 = 2x (x – 12) + 25 (x – 12)

0 = (x – 12)(2x + 25)

So,

x=12; x-12=0

x=-25/2 = -12.5; (2x+25) = 0.

As a result, the provided equation has two roots: 12 and -12.5.

Conclusion:-

Quadratic functions have a unique place in the educational system. They’re functions whose values can be approximated readily from input values, therefore they’re a step up from linear functions and a far way from straight line attachment.