Profile
Settings
Refer your friends
Sign out
Many of you may be familiar with the binomial theorem, particularly those who studied mathematics in high school, and those of you who do not will learn everything there is to know about it in this article. Let’s take a closer look at the term “Binomial Theorem/ Expansion.” Binomial Expansion is the expansion of that sum of two terms, and Binomial implies sum or difference of two terms. Now that we know what the literal meaning is, we can go on to some maths.
Binomial Theorem
The expanded value of an algebraic expression of the form x+yn is determined using the binomial theorem. It’s simple to calculate the value of x + y² x + y³, a + b + c² simply multiplying the exponent value by the number of times. However, calculating the
expanded version of x+y17 or other expressions with greater exponential values necessitates a significant amount of computation. The binomial theorem can help. The binomial theorem expansion’s exponent value might be a fraction or a negative number. Only non-negative numbers are considered in this section.
The binomial theorem was first mentioned in the 4th century BC by Euclids, a great Greek mathematician. The binomial theorem explains how to expand the algebraic statement (x + y)n into a sum of terms using individual exponents of the variables x and y. A numeric value called coefficient is assigned to each term in a binomial expansion.
According to the binomial theorem, any non-negative power of binomial (x + y) can be expanded into a total of the form,
Each nCk is a positive integer known as a binomial coefficient, and n≥0 is an integer.
Example
Let’s use the binomial theorem to extend x+35. Here, y equals 3and n equals 5. We get: by substituting and expanding:
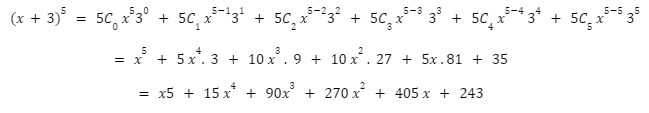
Solved examples of Binomial Theorem related questions
Calculate the third term of expansion 3 + y6.
Ans. Here r=3 and n=6.
So 3rd term of expansion 3 + y6 is calculated as
: 3 + y6 = 36-3+1 . y3-1 . [(6×5)/2]=34 . y² . 15 = 1215 y²
Example 2
Calculate the value of x if fifth term will be given is 105
Ans. -16 . 10c4 1 /2 √x6124 = 105 => x³ =10c4/105.210x = 1/8
Importance of Binomial Theorem in maths
The binomial theorem says we don’t have to add a number of binomial expressions together whenever we need to extend a+bn. Nowadays, kids take symbolic algebra programmes like Mathematica or Maple for granted, but back in the day, the B.T. could save a lot of time doing algebra (and be more accurate to boot, avoiding a lot of mistakes which might otherwise go undetected). The binomial coefficients are also the same as the entries in Pascal’s triangle, and the first two rows of the triangle can be used to calculate these entries using a simple technique.
Someone realised that multiplying a series of similar monomials together provided definite coefficients to the various terms in the product, hence the binomial theorem was born. These coefficients were later discovered to have a relationship with the amount of possible combinations when selecting two or more objects. When the binomial theorem was extended to non-negative integer exponents, new properties were revealed. There are many things in mathematics that have no or very little practical application, but it’s nice to have them on the shelf in case you need them.
Conclusion
The theorem is useful for finding permutations, combinations, and probabilities in algebra. The theory was known to Islamic and Chinese mathematicians in the late mediaeval period for positive integer exponents, n. Al-Karaj calculated Pascal’s triangle around 1000 CE, and Jia Xian calculated Pascal’s triangle up to n=6 in the mid-11th century. The broad form of the theorem (for any real number n) was found about 1665 and stated in 1676 without proof, with a proof by John Colson published in 1736. The theory can be extended to include complex exponents for n, which was demonstrated for the first time by Niels Henrik Abel in the early 1800s.
