How to Calculate the Length of Diagonal of a Square

A square is a two-dimensional plane figure that can be found in Geometry. It has four sides that are all the same length, and each of its four angles is equal to 90 degrees. The characteristics of a rectangle are relatively comparable to those of a square; however, the key distinction between the two is that a rectangle has equal sides only on its opposite sides. Because of this, a rectangle may only be referred to as a square if all four of its sides have the same length. 

Square: 

A square is an example of a regular quadrilateral, which is a shape that has four sides that are all the same length and angles that are all the same degree. All four corners of the square have a measure of 90 degrees, making them right angles. In addition to this, the diagonals of the square are parallel to one another and meet at right angles. One alternative way to define a square is as a rectangle with two sides that are the same length on opposite sides. 

The illustration on the right depicts a square in which all four sides are the same length and each angle is equal to 90 degrees.

A rhombus, which is also a convex quadrilateral and has all four sides equal, can be considered a square in the same way as a rectangle can if its vertex angle is right, just like a square is the same as a rectangle.

In the same vein, a square can be formed from a parallelogram if it has two neighbouring sides that are equal and a vertex angle that is correct. 

Shape of square: 

A square is a type of polygon with four sides that is characterised by having parallel sides of equal length and angles that have a measure of 90 degrees. The configuration of the square is such that if it were to be split along the middle by a plane, then both of the resulting halves would be symmetrical. When the square is cut in half, each half takes the shape of a rectangle with parallel sides that are equal in length. 

Properties of a square: 

The following is a list of the four most important characteristics of a square:

1. There is a 90-degree angle in each of the four internal corners.
2. Each of the square’s four sides is congruent with, or equal to, the other three sides.
3. The sides of the square that are opposite one another are parallel to one another.
4. The diagonals of the square cross one another at an angle of 90 degrees.
5. Both of the square’s diagonals are parallel to one another and have the same length.
6. The square has four points of intersection and four sides.
7. The diagonal of the square separates it into two isosceles triangles that are identical to one another.
8. The length of the square’s diagonals is greater than the length of any of its sides. 

Diagonal of a square: 

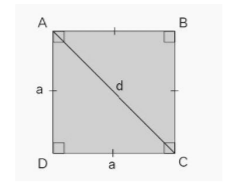
Each of a square’s diagonals is generated by connecting the opposing corners of the square, so a square has a total of two diagonals. Take note of the following square to help you make sense of the information regarding the qualities of the diagonals that are provided below.

1. The lengths of the diagonals in a square are identical to one another.
2. They cut each other in a manner that is perpendicular to the other.
3. They create two triangles that are congruent and isosceles with right angles out of the square. 

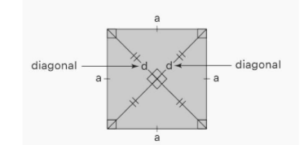
Diagonal of the square formula: 

The formula for determining the diagonal of a square is d = a√2, where’d’ refers to the diagonal and ‘a’ refers to a side of the square. Pythagoras’s theorem is used to obtain the formula for a square’s diagonal, which can then be used in square-foot calculations. A square can be cut into two triangles with isosceles and right angles if you use a diagonal. Both diagonals are identical, and they cross each other at right angles to form a perfect square. 

Derivation of diagonal of the square formula: 

Both diagonals in a square are the same length since a square is a square. The Pythagorean theorem can be used to determine the length of a square’s diagonal, denoted by the letter d, given its side length, a. When you examine the following square, you will notice that the length of the diagonal is represented by the letter ‘d,’ but the length of the side is represented by the letter ‘a.’ 

Diagonal of a square formula: 

Let us consider the triangle ADC in the square. We know that all the angles in a square are 90°, therefore, using the Pythagoras theorem, we can find the hypotenuse, which is ‘d’ in this case.

d² = a² + a²

d = √(a² + a²)

d = √(2a²)

d = √2 × √a²

= √2a

Therefore, the diagonal of a square formula is: d = a√2 

Significance of diagonal of a square: 

Each diagonal cuts the square into two congruent isosceles right triangles, which are special right triangles with 45, and 90-degree angles. A triangle like this has an area that is equal to one-half that of a square, its legs are squares, and the length of its hypotenuse is equal to the length of the diagonal of a square. 

Conclusion: 

A square’s diagonal is a line segment that connects any two vertices that are not next to one another. A square has two diagonals that are the same length and bisect each other at right angles. These diagonals are equal to one another. When the lengths of the sides of a square are already known, the formula for the diagonal of the square can be used to determine the length of the diagonal of the square.