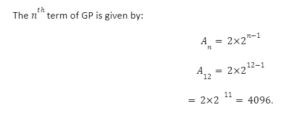Geometric progression, or G.P., belongs to the group of progressions, which are mathematical sequences in which each following phrase is generated by multiplying the preceding term with a set fixed integer. The term ‘sequence’ refers to a collection of items that are organized in such a way that each of them can be identified individually. A progression occurs when a series in a mathematical application follows a predefined pattern that may be established by calculations.
It’s a set of numbers in which each number is obtained by multiplying or dividing the previous number by a constant number. The common ratio of the series is the constant number.
A geometric progression is a set of numbers that have a common ratio between them. A positive or negative integer or fraction is the common ratio. It can be either a finite or infinite series.
Geometric Progression
Geometric progression is a special sort of number series sequence. The common ratio is a set of numbers in which each term is obtained by multiplying the previous term by a specified amount.
A geometric progression’s common ratio is a positive or negative integer. G.P. is the abbreviation for geometric progression.
Real-time Examples:
Calculating the bank’s interest earnings
Population increase
Terms Used in Geometric Progression
We will use specific terms in geometrical progression (G.P.) to answer the mathematical problems listed below:
a – First term
r – Common Ratio
an–nth Term
Sn – Sum of n terms (Finite)
S – Sum of terms (Infinite)
Formula of Geometric Progression
Each term in a geometric progression is obtained by multiplying the previous term by a set number (common ratio).
In general, the progressions are written as follows:
a, ar, ar2, ar3,……
Except for the first term, each term is derived by multiplying the previous term by the common ratio.
a-First-term
r-Common ratio is used here
Geometric Progression- First Term
The word is the name given to each number in a series. The first number of the given series is the first term of the G.P. As a result, the first term of the G.P. is known as the starting or initial number.
It’s usually written as a1 or a.
Example:
Series 6, 12,24,48,96……
The initial term is 6.
Geometric Progression- Common Ratio
Geometric progression is a set of integers in which each number is obtained by multiplying or dividing the preceding number by a fixed amount. The common ratio of the series is the constant number.
Except for the first term, the geometric progression, in which each value is derived by multiplying with the common ration r, is presented below:
Now, the Common ratio is getting by dividing the term by its preceding term except the first or initial term. Such as:
r=a1ra1=a1r2a1r=a13a1r2
Hence, the General Formula is r=anan-1.
Properties of Geometric Progression
There are several undiscovered aspects of geometric progression that assist in the simple solution of mathematical issues. The following are a few of them:
When each term of a geometric series is multiplied by a non-zero constant number, the result is a new series with the same common ratio.
When we divide each term of the geometric series with the non-zero constant number, the resulting series also forms geometric series with the same common ratio.
The reciprocal series of geometric progression terms is also a geometric series.
The new series likewise creates geometric series when each term of the series changes to the terms’ square.
The new series is geometric when the terms of a geometric progression are selected at intervals.
Each term of geometric progression (non-zero, non-negative series) becomes an arithmetic series when the logarithm is changed.
Tricks for Geometric Progression
Follow these strategies to solve many sorts of geometrical progression mathematics problems quickly:
Consider the integers ar,a,ar, where r is the common ratio, where the product of three geometric progression terms is supplied.
Consider the integers ar3,ara,ar3 when the product of four geometric progression terms is supplied, where r is the common ratio.
Consider the integers ar2 ,ara,ar,ar2, where r is the common ratio, when the product of five terms of the geometric progression is given.
Conclusion
We looked at the definition of geometric progression in this article, which is a collection of numbers connected by a common ratio. The first term, common ratio, and nth term of the geometric progression, as well as the formulas, have all been examined.
We’ve looked at finite and infinite series, as well as the formulas for calculating the geometric progression’s sum of terms. This article explored the properties of geometrical progression as well as several problem-solving techniques. Solved examples are used to explain some of the principles.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out