Find the Area of Rectangle

The space that any closed figure sweeps or covers is referred to as the area. The area of a given figure is the area that lies within its perimeter. This leads us to the conclusion that the area of a rectangle is the region that it sweeps or covers. In other words, a rectangle’s area is the two-dimensional area contained within its perimeter. 

Area of a Rectangle Formula:

One of the simplest mathematical formulas is the one we will study now, which calculates the area of a rectangle. Despite being straightforward, it is also one of the most effective formulas. This formula was solely used to get the area between the table you are studying and the room you are living in.

The formula for rectangle area is as follows:

Area = length x width or length

We can calculate the area of a rectangle using the product of its length and breadth. Area “A” is written as though the rectangle’s length were “a” and its width were “b.”

A = a x b (square units)

Calculating the Area of a Rectangle:

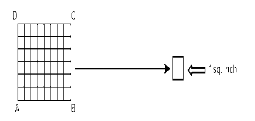
We utilize the unit squares to calculate a rectangle’s area. As indicated, divide the rectangle ABCD into unit squares. The total number of unit squares that make up a rectangle ABCD is its area.

ABCD rectangle in unit squares, each measuring one square inch

As a result, the rectangle ABCD has a total area of 48 square inches.

Using this method, we also discover that the area of a rectangle is always equal to the sum of its two sides. 

Here, AB measures 8 inches in length while BC measures 6 inches. The result of multiplying 6 by 8 is 48, which is the area of ABCD.

Since the lengths are multiplied together, the measurement will be in “square inches.”

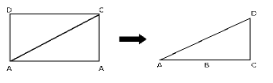
An alternative method for calculating a rectangle’s area is to divide it into two right triangles of equal size. For instance, a diagonal is drawn from vertex A to vertex C in the rectangle ABCD that is given.

The rectangle is split into two identical right-angled triangles by the diagonal AC.

Thus, the area of ABCD will be:

      ⇒ Area (ABCD) = Area (ABC) + Area (ADC)

      ⇒ Area (ABCD) = 2 × Area (ABC)

      ⇒ Area (ABC) = 1⁄2 × base × height

      ⇒ Area (ABCD) = 2 × (1⁄2 × b × h)

      ⇒ Area (ABCD) = b × h

Steps on how to Calculate Area of Rectangle?

The steps for calculating a rectangle’s area are listed below. You won’t ever have a problem with faults in your solutions if you carefully follow these procedures.

Step 1: note the dimensions of the rectangle that was provided in the questions.

Step 2: Enter the values into the length x width rectangular area formula.

Step 3: Multiply the values to obtain the result.

Step 4: Write the outcome in square units .

Example:

Consider the following example to better understand how to determine a rectangle’s area. We will determine the area of a rectangle with dimensions of 20 units in length and 5 units in width.

Step 1: Given that the rectangle’s length is 20 units and its width is 5 units

Step 2: Use the formula area of rectangle = length x breadth.

Step 3: 20 x 5 = 100

Step 4: The rectangle has a 100-square-unit area.

Area of a Rectangle by Diagonal:

Area of a Rectangle by a Diagonal: As was already established, a rectangle is split into two right-angled triangles by a diagonal. We’ll figure out a formula to calculate a rectangle’s area using diagonals utilizing the Pythagoras theorem.

The Pythagorean Theorem states:

(Hypotenuse)² = (Base)² + (Perpendicular height)²

In this instance

Give the dimensions diagonal (d), length (l), and width (b).

(Length)² + (Breadth)² = (Diagonal)²

(d)² = (l)² + (b)²

(l)² = (d)² – (b)²

l = √(d)² – (b)²

changing the l value in the primary formula

L x B equals the rectangle’s area.

= {(d)2– (b)2} x b

The area of a rectangle is therefore (d)² – (b)2x b = (Diagonal)² – (Breadth)² x Breadth when the length of one diagonal and the dimension of breadth are given.

Conclusion:

In two dimensions, an object must have been measured for length and breadth. Here, the length and breadth of a rectangle are not equal. A rectangle’s area is calculated by multiplying the length by the width of its two sides. The rectangle’s area is measured in square units.

The area of a rectangle has several fascinating uses, such estimating the height of a skyscraper and computing the area of a rectangular floor.