Find the Angles and the Area of Trapezium

A trapezium is a convex quadrilateral with one pair of opposite sides that are perfectly parallel to one another. When sketched on a sheet of paper, the trapezium looks like a table. A quadrilateral is a polygon with four sides and four vertices in Euclidean geometry. A trapezium has four sides, four angles, and four vertices as a result. The trapezium rule, in which the area under the curve is divided into a number of trapeziums and the area of each trapezium is evaluated, is a common application of trapezium.

Finding the angles of trapezium

We know that the total of all internal angles for any quadrilateral is 360 degrees. As a result, if an angle x is given between one parallel and one non-parallel side, subtracting twice of this angle from 360 yields the sum of two angles on the formed opposite side of x. Once the sum has been calculated, divide it by two to get the fourth angle’s measurement.

Example: A trapezium’s base angle, including the angle between parallel and non-parallel sides, is 110 degrees. Then get the angle that is the polar opposite of the provided angle.

Let, the unknown angle is A

Given angle=110

As we know the property,

Subtract 110 × 2 from 360,

360 – 220 = 140

Now, 140 is the sum of above 2 angles

Thus, A = 140/2=70 is the opposite angle of the provided one.

Area of trapezium

The area of a trapezium is measured in square units and is defined as the number of unit squares that can fit into it. A trapezium is a quadrilateral with one parallel pair of sides. Legs are the opposite pair of sides of a trapezium that might be non-parallel. The total area covered by a trapezium in a two-dimensional plane is called its area.

The lengths of two parallel sides of a trapezium and the distance (height) between them can be used to compute the area of the trapezium. The formula for calculating the area (A) of a trapezium using the base and height of the trapezium is as follows: 

A = ½ h(a+b)  square units.

Where, a and b = bases of trapezium, and, h = height (the perpendicular distance between a and b)

Area of Isosceles Trapezium

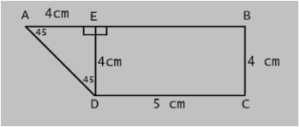
Let a and b denote the lengths of parallel sides of a trapezium ABCD, where a denotes the base length and b denotes the length of a parallel side.

Then, a>b

Now, let h be the height of an isosceles trapezium, and c be the length of two non-parallel sides.

So, AB = a, CD = b, BC = AD = c

If we draw a perpendicular h from CD to meet AB at E, we get AED, which is a right triangle.

Hence, Length of perpendicular, h = √(c²– (a-b)²)

As we know, Area = ½ h(a+b)

Area of isosceles trapezium = ½ [√(c²– (a-b)²) (a+b)]

Perimeter of trapezium

The perimeter of the trapezium is the total sum of the length of the border produced by the sides of the trapezoid or trapezium. It is a skewed polygon. Because all of the lines and vertices are contained in the two-dimensional plane, the trapezoid’s perimeter is contained in the two-dimensional shape.

Assume that we have a trapezoid ABCD with sides AB and CD parallel to each other. While AD and BC are non-parallel sides, they form the pair’s ‘bases’ (that is, they are legs). Assume that the trapezoid’s perimeter is identical to “P” units.

The perimeter of trapezoid ABCD is given by,

P = AB + BC + CD + AD. 

The perimeter of the trapezoid in terms of area is given by the following formula,

P = sum of the lengths of non-parallel sides+ 2(A/h)

where A is the area of trapezoid and h is its height.

Conclusion 

In this article we proved the area and perimeter of a trapezium. When sketched on a sheet of paper, the trapezium is a two-dimensional object that looks like a table. In actual life, there are numerous trapezium examples. The trapezium rule, which divides the area under the curve into a number of trapeziums and then evaluates the area of each trapezium, is a popular use of trapezium.