Profile
Settings
Refer your friends
Sign out
A line segment that connects any two of a rectangle’s non-adjacent vertices is said to be its diagonal. A diagonal divides a rectangle into two right triangles, each of which has a hypotenuse and sides that are equal to the sides of the rectangle while the diagonal is the hypotenuse.
Formula for rectangle’s diagonal
The formula for calculating a rectangle’s diagonal length is
d = √(l² + w²)
where,
l stands for the rectangle’s length.
w is the rectangle’s width.
Derivation of the diagonal of a rectangle:
The Pythagorean theorem is used to derive the diagonal of a rectangle formula. Consider a rectangle that is “l” length and “w” width.
Let d represent the length of each diagonal.
When the triangle ABD is subjected to Pythagoras’ Theorem,
D2 = l² + w²
square roots on each side,
d = √(l² + w²)
The formula for a rectangle’s diagonal is as follows:
d = √(l² + w²)
where,
l stands for the rectangle’s length, w is the rectangle’s width.
Properties of diagonal:
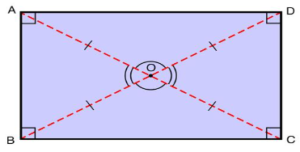
- The two diagonals are congruent (identical in length); in this case, the diagonals are AC and BD, and AC equals BD.
- The diagonals equally cut each other in half; in this case, AC and BD do so.
- Each diagonal splits a rectangle into two identical right-angled triangles; in this case, AC splits ABCD into two ABCs and an ADC, and BD splits ABCD into two BCDs and a BAD.
- The diagonals are not parallel to one another; in this case, diagonals AC and BD are not parallel.
- At the point of contact, the adjacent central angles are not equal, but the opposing central angles are; in this case, AOB = COD & BOC = AOD, but AOB AOD or BOC, & BOC COD or AOB.
Measurement of a diagonal:
Any shape’s diagonal length is a function of the size of its sides.
Square’s diagonal length
The Pythagoras theorem can be used to determine how long a square’s diagonal should be. A square is split into two right-angled triangles by a diagonal. We can get the length of the diagonal (d) of a square with side (a) as a by using the Pythagoras theorem.
square’s diagonal length when each side is a unit long equals a unit.
Length of the rectangle’s diagonal
A rectangle is split into two right-angled triangles by a diagonal. In a rectangle of length (l) and breadth (b), we may use the Pythagoras theorem to determine the length of the diagonal.
d = l + b
As a result, d =, where d is the rectangle’s diagonal, l is its length, and b is its width.
Diagonal History:
The ancient Greek phrase diagonios, which means “from angle to angle,” is where the word diagonal first appeared. It was used by Euclid and Strabo to refer to a line that joins two cuboid or rhombus vertices; it eventually acquired the Latin name diagonus (slanting line).
Polygonal Diagonals:
There is a formula to calculate the number of diagonals for polygons of any shape, including those of any size.
In a polygon with n vertices, the number of diagonals is equal to n(n-3)/2.
Conclusion:
The line segments connecting the opposite corners or vertices of a rectangle form its diagonal.The line that crosses the centre of the rectangle and extends from one corner of the rectangle to the other is known as the diagonal. Diagonals are lines that connect two non-adjacent polygonal vertices, i.e., two vertices of the figure without the polygon’s sides. The diagonal formula is used to calculate diagonals.
