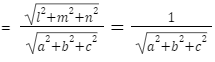3D geometry is the study of shapes in three-dimensional space using three coordinates: x-coordinate, y-coordinate, and z-coordinate. To discover the precise position of a point in three dimensions, three criteria are necessary.
Three-dimensional geometry is important for CAT because it is covered in many questions. The basic ideas of geometry involving three-dimensional coordinates are covered here, which will aid in understanding different operations on a point in the three-dimensional plane.
Coordinate System
A coordinate system is the technique of determining the position of a point on the coordinate plane in three dimensions.
Rectangular Coordinate System
Three parallel lines intersect at a common place. The origin is the common point, and the three lines are the axes. They are the x-axis, y-axis, and z-axis. The observer’s position in relation to other point is quantified by O.
The location or coordinates of every point in three-dimensional space are determined by how far he has travelled along the x, y, and z-axes. So, a point with the coordinates (3, -4, 5) has travelled 3 units along the positive x-axis, 4 units along the negative y-axis, and 5 units along the positive z-axis.
Distance from the Origin
The distance P (x, y, z) from origin (0,0,0) is given by √(x2+y2+z2)
Distance between Two Points
The distance between the two points P (x1, y1, z1) and Q (x2, y2, z2) is formulated as
√[(x2-x1)2 + (y2-y1)2+ (z2-z1)2]
The mid-point R of a line is given by
Direction Cosines and Direction Ratios of a Line in the Cartesian Plane
The direction cosines of a line are the cosines of the angles it makes with the positive x, y, and z axes, respectively.
So, if those angles are α, β, ϒ then cosα, cosβ, cosϒ are the direction cosines of the line. They are denoted as l, m, n.
l2+m2+n2 = 1
The 3 numbers a, b, c which are proportional to the direction cosines are called as direction ratios.
So, l/a = m/b = n/c
Direction Cosine of Line Joining Two Given Lines
Let P (x1, y1, z1) and Q (x2, y2, z2) be the two points. Then direction cosines will be
l = (x2–x1)/|PQ|, m= (y2-y1)/|PQ| ,n = (z2-z1)/|pQ|
Projection of Line Segments Joining Two Points on Another Line
P(x1y1z1) and Q(x2y2z2)
The projection of P, Q on a line whose direction cosines are l, m, n is given by
|(x2 – x1) + m (y2 – y1) + n (z2 – z1) |
Angle Between Two Lines in 3- Dimensional Space
The two lines having direction cosines given as (l1, m1, n1) and (l2, m2, n2). Then angle between them is
ϴ = cos-1(l1l2 + m1m2 + n1n2)
3- Dimensional Geometry Concepts for CAT
Mathematicians have been investigating and articulating meaningful findings to simplify geometry for years. Since then, it has been an integral element of our curriculum since the beginning of middle school, despite the fact that the concepts taught in early middle school are much simpler and basic than those taught in high and secondary school.
Due to the inevitability of deeply embedded Geometric principles, it plays an important role in the course framework of numerous competitive tests just like CAT, XAT, SSC, BANK PO, and others. Every year, almost 4-5 questions on this subject of mathematics are asked, ranging in difficulty from medium to challenging.
Geometry is the branch of mathematics concerned with deducing the qualities, measurements, and relationships of points, lines, angles, solids, & figures in space from their establishing conditions using certain assumed spatial properties.
Mensuration is the process of calculating the total surface area, lateral/curved surface area, and volume of 3D solids.
Ratio of Intercepts
If a transversal intercepts three parallel lines, the ratio of intercepts formed equals the ratio of intercepts formed by any other transversal, ab=cd=ef, where a, b, c, d, e, and f are intercepts.
Theorem of Appolonius
If AD is the median from point A to length BC in a triangle ABC, then AB2 + AC2= 2 (AD2 + BD2).
Formula of Heron
If the sides of a triangle are a, b, and c, half perimeter (s) = (a + b + c)/2, and the triangle’s area is:
Area = √ {S (S – a) (S – b) (S – c)}
Triangle Area Calculated Using Trigonometry
If the three sides of a triangle are a, b, and c, and the three angles are A, B, and C, the triangle’s area is 1/2 bc x sinA or 1/2 ab x sinC or 1/2 ac x sinB.
Theorem of Pythagoras
If ‘a’ & ‘b’ are two triangle sides other than the hypotenuse, then c2 = a2 + b2.
Circle
The circle area of geometry covers a wide range of issues, including common tangents, the angle formed by secants in a circle, direct & transverse common tangents, and so on.
Geometry in 3D
Under 3D geometry, total/lateral surface area, volume, slant height, and other properties of various forms such as a hemisphere, frustum, cone, cylinder, and so on are calculated.
Geometry of Coordinates
Coordinate geometry includes line equations, quadrants, slope intercepts, and graphical representations of lines, among other things.
Importance of Geometry in CAT Exam
Geometry aids us in deciding the materials to employ when constructing a structure in real life. It also aids in the design of structures. Geometry test questions on the CAT will assess your knowledge of geometric shapes.
The CAT exam will likely include 4-6 geometry questions. In competitive tests, this reasonable no. of questions might make all the difference.
Each CAT question is worth three points. You don’t want to lose any marks on the CAT exam because of geometry questions.
Geometry questions in the CAT examination will also evaluate your math skills and problem-solving ability.
CONCLUSION
Computer-aided design (CAD) for construction plans, design of assembly systems in manufacturing such as vehicles, nanotechnology, computer graphics, visual graphs, video game programming, & virtual reality development are all examples of real-world applications of geometry.
One of the most significant topics in the CAT Quantitative Aptitude section is geometry. Circles, parallel lines, and triangles are among the concepts that must be practised concurrently with coordinate geometry, with the congruency & similarity of triangles being particularly highlighted.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out