Venn Diagram Questions

A Venn diagram is a graphic that employs circles to represent relationships between objects or finite groups of objects. Circles that overlap share qualities, whereas circles that do not overlap do not.

Venn diagrams are used to understand the similarities and differences between two concepts visually. They’ve long been acknowledged for their educational value. Venn diagrams have been utilised in introductory logic curriculum and elementary-level educational plans all across the world since the mid-20th century.

Application

Venn diagrams are used to show how elements relate to one another against a backdrop, universe, data set, or environment. For example, a Venn diagram may be used to compare two companies in the same industry by demonstrating the products that both companies offer (where circles overlap) as well as the products that are distinctive to each company (outer circles).

Venn diagrams are basic graphical representations of the relationship between two groups of objects. They can, however, be far more complicated. Despite this, the Venn diagram’s streamlined aim of illustrating concepts and groups has led to its widespread use in a variety of sectors, including statistics, linguistics, logic, education, computer science, and commerce.

Formulas

Some important formulas for two and three elements in the Venn Diagram.

n ( A ∪ B) = n(A ) + n ( B ) – n ( A∩ B)

n (A ∪ B ∪ C) = n(A ) + n ( B ) + n (C) – n ( A ∩ B) – n ( B ∩ C)

 – n ( C ∩ A) + n (A ∩ B ∩ C)

where n( A) = number of elements in set A.

Questions

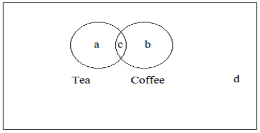
1)In a college, 200 students are chosen at random. 140 people enjoy tea, 120 people enjoy coffee, and 80 people enjoy both tea and coffee.

How many students are only interested in tea?

How many people are solely coffee drinkers?

How many students don’t care for either tea or coffee?

How many students are content with just one cup of tea or coffee?

How many of the people enjoy at least one of the drinks?

Solution:

The following Venn diagram can be used to represent the supplied information, where T represents for tea and C for coffee.

The number of students who solely drink tea is 60.

There are 40 students that solely drink coffee.

There are 20 students that do not like tea or coffee.

60 + 40 = 100 students like only one type of tea or coffee.

Number of students that enjoy tea or coffee = n (just tea) + n (only coffee) + n (both tea and coffee) = 60 + 40 + 80 = 180

2. A survey of 500 college students indicated that 49 percent of them enjoyed watching football, 53 percent like hockey, and 62 percent enjoyed basketball.Furthermore, 27 percent like both football and hockey, 29 percent enjoyed both basketball and hockey, and 28 percent enjoyed both football and basketball. None of these games appealed to 5% of the population.

How many students enjoy watching all three games at the same time?

Calculate the proportion of students who prefer to watch only football versus those who prefer only hockey.

Calculate the number of students who prefer to watch only one of the three games.

Determine how many students enjoy watching at least two of the games.

Solution: n(F) = fraction of students who enjoy watching football = 49%

n(H) = number of students who enjoy watching hockey = 53%

n(B) = 62 percent of students who enjoy watching basketball.

(F H) = 27%; (B H) = 29%; (F B) = 28%

Because 5% of people prefer not to watch any of the games, n (F H B) = 95%.

95 percent = 49 percent + 53 percent + 62 percent -27 percent – 29 percent – 28 percent + n (F H B) Solving gives n (F H B) = 15 percent.

Create a Venn diagram using the values provided.The Venn diagram’s values are all in percentages.

Adding all three games equals 15% of 500 = 75.

The ratio of pupils who only like football to those who only like hockey is (9 percent of 500)/(12 percent of 500) = 9/12 = 3:4.

The total number of students who choose to watch only one of the three games is 205 (9 percent + 12 percent + 20 percent).

(number of students who enjoy watching only two of the games) + (number of students who enjoy watching all three games)= (12 + 13 + 14 + 15) percent, or 54 percent of 500 = 270.

Conclusion

Using visual tools to solve Venn Diagram questions makes it simple. Distinct sections can be shaded or marked to represent different groups or sets. However, it is important to emphasise that the existence or absence of any relationship between the supplied quantities should be properly marked.