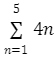Types of Series

A series is a definition of the operation of adding infinitely multiple quantities, one after the other, to a specified initial quantity in mathematics. Calculus and its generalisation, mathematical analysis, both include the study of series. Series are utilised in almost all fields of mathematics, including generating functions for investigating finite structures (like in combinatorics). In current language, any (ordered) infinite sequence of terms (be it, numbers, functions, and anything that can be added) refers to a series, which is the operation of adding the ai one after the other. A series might be dubbed an infinite series to stress that there are an infinite number of terms. An expression like represents (or denotes) such a sequence,   a1 + a2 + a3 + a4 +………

or, using the summation sign,

Series

A series implies an unending sequence of additions that cannot be carried out efficiently (at least in a finite amount of time). If the set to which the terms and their finite sums correspond to a notion of limit, however, it is occasionally possible to assign a value to a series, which is known as the sum of the series. This value represents the limit of the finite sums of the n initial terms of the series, also known as the nth partial sums of the series, as n approaches infinity (if the limit exists). In other words, when this limit is reached, the series is said to be convergent or summable, or the sequence (a1 , a2 , a3 , a4 ). The sum of the series is the limit in this case. The series is otherwise described as diverse. The notation

signifies both the series—that is, the implied process of adding the terms one after the other continuously, if the series is convergent, the sum of the series—the process’s result. This is an extension of the comparable convention of indicating both the addition—the process of adding, and the result, the sum of a and b—by a + b. 

Number Series

A series is a logical arrangement of figures, numbers, words, or alphabets. A number series is a collection of numbers that follow a specific pattern. Some specific pre-determined rules are concealed in number series questions, and the candidate must identify them to arrive at the proper answer.

Consider the numbers 1, 4, 7, 10, 13… The difference between the two successive numbers is three in this case. It’s worth noting that in a number series, every number except the first is related to the previous number according to a set of rules.

Types of Number Series

Some of the types of number series are discussed below:

Arithmetic Series

The total of the terms of an arithmetic sequence is called an arithmetic series. A geometric series is the sum of a geometric sequence’s terms. Other sorts of series exist, but you won’t have much experience with them until calculus. For the time being, you’ll most likely be working with these two. This page demonstrates and explains how to use arithmetic series.

You can only take the “partial” sum of an arithmetic sequence for reasons that will be described in calculus. The partial sum is the sum of a small (that is, finite) number of terms, such as the first ten or the fifth through the hundredth terms. Starting with, i = 1, the formula for the first n terms of an arithmetic sequence is:

The sum of the first ‘n’ terms of a series is known as “the nth partial sum”, and is commonly denoted as “Sn”.

Geometric Series

A geometric series refers to the sum of an infinite number of terms with a constant ratio between them in mathematics. For instance, consider the series 

1/2 + 1/4 + 1/8 + …

is geometric because each subsequent term can be produced by multiplying the preceding term by ½. Commonly a geometric series can be written as a + ar + ar2 + ar3 +….. in this a is the coefficient of each term and r is the common ratio of nearby terms. Geometric series are among the simplest infinite series, and they can be used to learn about Taylor and Fourier series. Geometric series were crucial in the early stages of calculus development.

Each term in a geometric series is the geometric mean of its two neighbouring terms, similarly to how each phrase in an arithmetic series is the arithmetic mean of its two neighbouring terms. A geometric sequence or, equivalently, a geometric progression is a sequence of geometric series terms (without any additions).

Addition Series

Summation is the addition of a sequence of any form of numbers, called addends or summands, with the result being their sum or total in mathematics. Other sorts of values, in addition to numbers, can be summed: functions, vectors, matrices, polynomials, and, in general, members of any form of mathematical object that has the “+” operation defined. Series are summations of infinite sequences. Summation or sigma notation can be used to represent a series in a concise format. The sum is represented by the Greek capital letter ∑

The series 4 + 8 + 16 + 20 can be expressed as

The expression is read as the sum of 4n as n goes from 1 to 5. The variable n is called the index of summation.

To generate the terms of a series given in sigma notation, successively replace the index of summation with consecutive integers from the first value to the last value of the index. To generate the terms of the series given in sigma notation above, replace n by 1, 2, 3, 4, and 5. 

= 4(1) + 4(2) + 4(3) + 4(4) + 4(5)

= 4 +8 + 12 + 16 + 20

= 60

Thus, the sum of the series is 60.

Conclusion

The notions of sequence and series are key in Arithmetic. A series is the sum of all elements, but a sequence is an itemised collection of elements that allows for any sort of repetition. The mathematical progression is one of the most common examples of sequence and series. A sequence is a collection of items or objects that are generally arranged in a precise order. A series can be generalised by adding up all of the terms in it. All of the sequence’s terms, however, must have a clear link. The principles can be better understood by solving issues using formulas. They’re similar to sets, but individual terms in a sequence may appear more than once in different positions. The length of a sequence is equal to the number of terms it contains, and it might be limited or infinite.