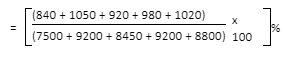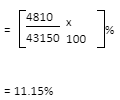A table chart is a set of data that is organised in rows and columns and is one of the most common ways to communicate information to others. A table is made up of numerous boxes, each containing information. The titles are usually indicated by the first row and first column.
While every sort of data can be displayed in table form, and with great accuracy, comprehending the data in table form is more complex and time consuming than the other modes, which are all primarily pictorial or graphical in nature.
This part contains questions in which data from common fields such as production is presented in the form of a table over a period of several years: imports, exports, factory employee incomes, students applying for and qualifying for a specific field of study, and so on.
The candidate must first comprehend the provided material before answering the questions based on a comparative examination of the facts.
Tips for Solving Table Chart Problems:
- Carefully read the data, as even the tiniest detail can radically change the meaning of the question.
Similarly, the instructions must be carefully read to avoid wasting time computing data that isn’t required and to determine exactly what the desired solution is.
2.Before answering the questions, make an effort to completely comprehend the information offered. The questions are designed to trick you, so be sure you understand the prerequisites. Try to comprehend the relationship between the given tables if the data is of a mixed kind or if there are multiple data tables/charts/graphs.
One table would discuss absolute sales data, while the other might discuss sales as a percentage of production. As a result, any enquiry about surplus production or goods in stock will necessitate information from both tables.
3. Pay close attention to the units in the tables, as well as the units in which the solutions (options) are given. A typo in the units could result in a completely different result.
Also, check whether the answer must be in decimal or percentage form. These kind of mistakes are prevalent and easily prevented.
Questions and answers on table reasoning:
Q.1)Look over the table below and answer the questions.
Over the years, the number of candidates who appeared and qualified in a competitive examination from various states has increased?
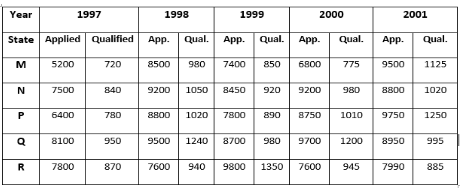
1)What is the proportion of candidates qualified to that of the candidate appeared when the states P and Q are combined in 1998?
A. 10.87%
B. 11.49%
C. 12.35%
D. 12.54%
E. 13.05%
Answer: C
Required percentage |
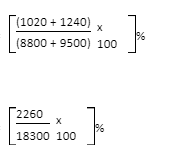
2)What was the average number of candidates from State Q who appeared in the provided years?
A. 8700
B. 8760
C. 8990
D. 8920
E. 8810
Answer: C
Required average.
= 8100+9500+8700+9700+8950 /5
=44950/5
=8990
3) What is the proportion of applicants qualified from State N for all years compared to the number of candidates who appeared from State N for all years?
A. 12.36%
B. 12.16%
C. 11.47%
D. 11.15%
None of these
Answer: Option D
Required percentage
Q.2)A school has four sections W,X,Y and Z of Class IX students.
The results of half sem and annual sem are shown in the table given below.
Result | No. of Students | |||
Section W | Section X | Section Y | Section Z | |
Students failed in both Sem | 28 | 23 | 17 | 27 |
Students failed in half-sem | 14 | 12 | 8 | 13 |
Students passed in half-sem | 6 | 17 | 9 | 15 |
Students passed in both sem | 64 | 55 | 46 | 76 |
1. Which of the following assertions is true in this context if the number of students passing a test is used as a criterion for comparing the difficulty level of two examinations?
A.Half-yearly exams were more challenging.
B.Annual exams were more challenging.
C.The examinations were nearly identical in difficulty.
D.The difficulty levels of the two exams cannot be compared.
E.The annual examinations appear to be more difficult for pupils in Sections A and B than the half-yearly examinations.
Answer: C
Explanation:
Number of students who passed half-sem exams in the school
= (Number of students passed in half-sem but failed in annual exams)
+ (Number of students passed in both sem)
= (6 + 17 + 9 + 15) + (64 + 55 + 46 + 76)
= 288.
Also, Number of students who passed annual sem in the school
= (Number of students failed in half-sem but passed in annual sem)
+ (Number of students passed in both sem)
= (14 + 12 + 8 + 13) + (64 + 55 + 46 + 76)
= 288.
Since, the number of students passed in half-sem= the number of students passed in annual sem.
Therefore, it can be inferred that both the sem had almost the same difficulty level.
Conclusion:
Tables and graphs are effective tools for organising data and making decisions. They can also be used to provide evidence to persuade others to support a particular viewpoint.
Developing arguments and making decisions requires thinking, analysing, and synthesising evidence from many sources.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out