The syllogism is an essential component of each and every aptitude test that students take. Logical reasoning encompasses this particular line of thought. Because of the air of mystery that surrounds them, syllogisms have worked their way up the ranks to become an essential component of ability tests over the years. In almost all Government examinations, the subject of syllogism is covered, and questions on the subject are invariably included in the test; this trend has been observed throughout the course of the past several years. Therefore, having a solid comprehension of the topic is of the utmost importance.
Syllogism:
The Greek term “syllogismos,” from which we get our word “syllogism,” literally translates to “conclusion” or “inference.” A syllogism is a form of logical argument that uses deductive reasoning to reach a conclusion. It consists of a series of statements. Aristotle is credited with making a significant contribution to the field of syllogisms through his work.
The questions that are asked in this part comprise two or more statements, and following these statements are either two or more conclusions or two or more additional statements. One has to choose which of these conclusions are the most reasonable ones given the statements that have been presented. The assertions have to be accepted as true, despite the fact that they may appear to go counter to the generally accepted facts.
There is more than one approach to solve problems using syllogisms. Utilizing a Venn diagram is by far the most successful and time-saving approach there is. Drawing every feasible diagram based on the assertions that have been provided, and then solving each of these diagrams one at a time, is the best way to proceed. In conclusion, the answer that is consistent throughout all of the diagrams is considered the correct one.
Statements of syllogism:
The syllogism questions consist of three primary components each.
Major premise
Minor premise
Conclusion
The primary assertion that serves as the central premise is one that the author holds to be generally accurate.
Example: All women are smart.
A particular illustration of the major premise is known as the minor premise.
Example: Amanda is a woman.
A particular assertion that logically follows both the main statement and any subordinate statements is the conclusion.
Example: Amanda is smart.
Applications of Venn Diagrams:
Draw the Venn diagrams in accordance with the major and minor assertions so that you may determine whether or not the stated conclusion is right.
The preceding is an illustration of the combination of large and small statements, presented in two distinct ways. In the first scenario, the assertion that “All women are smart,” the Venn diagram of women is contained within the Venn diagram that depicts smart. Therefore, the primary assertion is correct. And because Amanda is a woman, the circle in the Venn diagram that represents Woman should contain the Amanda circle. In the second scenario, the only distinction that can be made is that in the Venn diagrams for women and intelligence, the circles overlap in the second case. The major statement in this scenario is that all women are intelligent. Because this opens up even another avenue of thought. There is a representation of women inside it due to the fact that Amanda is a woman. After looking at both situations, we can conclude that “Amanda is smart” is correct because it can be proven from any scenario.
The conclusion must be valid when considered in light of all the different scenarios. Before coming to a decision, it is important to consider all of the different scenarios. Find, below the table, the correct combination of Venn diagrams consisting of major and minor premises.
Steps to solve syllogism questions:
Take note of the total number of variables that are included in the statements that are supplied.
Ex: Man, doctor, pilot, etc.
Create a Venn diagram for each variable, where the number of Venn diagrams should be equal to the number of variables.
Reading the statements will allow you to deduce the logical level, and then you can design the Venn diagram that corresponds to that level.
Verify the findings by contrasting the resulting Venn diagram with the one that was provided.
Choose the conclusion that best fits the situation.
Solved examples:
Instructions: Consider the following assertions, and then choose whether the conclusion is accurate or incorrect.
Example 1:
Major premise: All Actors are right-handed.
Minor premise: All right-handed are Artists.
The conclusion is: Some Artists are Actors.
Correct
Incorrect
Solution:
Explanation:
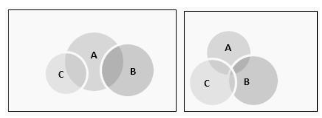
Case 1:
A right-handed Venn diagram is contained within an actor Venn diagram, which in turn is contained within an artist Venn diagram. The section of the red Venn diagram that overlaps with the green component of the figure suggests that some artists also work as actors, as indicated by the diagram. As a result, the conclusion is valid on the basis of this diagram; but, it cannot be accepted as the conclusive solution until the second scenario is investigated.
Case 2:
As a result of the fact that all of the Venn diagrams overlap with one another, the diagram suggests that all of the actors are also artists or all of the artists are also actors. The conclusion that “some artists are actors” is incorrect as a result of this. Owing to the fact that the conclusion is flawed in light of the second Venn diagram. The answer that is accurate is not option B, which is incorrect.
Conclusion:
The application of deductive reasoning is referred to as a syllogism, and the term syllogism is used to describe a particular type of argument. A syllogism is a type of logical argument that consists of two premises that are contrasted with one another in order to reach a conclusion.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out