Equations aren’t necessarily about being balanced on both sides with a ‘equal to’ symbol in mathematics. When something is bigger or smaller than the other, it’s called a ‘not equal to’ connection. An inequality is a relationship in mathematics where two numbers or other mathematical expressions are compared in an unequal manner. Inequalities are mathematical expressions that are classified as algebraic.
Let’s look at inequalities’ rules and how to solve and graph them.
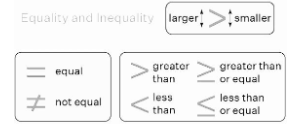
Definition
Inequalities are two-sided mathematical expressions having unequal sides. Unlike equations, we compare two values in inequality. Between the equal signs, a less than (or less than or equal to), greater than (or greater than or equal to), or not equal to sign is used.
Olivia was chosen for the 12U Softball team. Olivia’s age is unknown. Because it doesn’t mention “equals,” you don’t know Olivia’s age. Olivia’s Age 12 can be written if you know her age should be less than or equal to 12. This is a real-life incident with inequality.
3 ways to solve inequality
To transfer the variable to one side and isolate it, use addition, subtraction, multiplication, and division. You’ve solved the inequality after you’ve isolated the variable. When multiplying or dividing by a negative amount, reverse the inequality sign.
Solving Inequalities
The steps for resolving inequalities are as follows:
Step 1: Make an equation out of the inequality.
Step 2: Determine one or more values for the equation.
Step 3: On the number line, represent all of the values.
Step 4: Use open circles to indicate all omitted values on the number line.
Step 5: Determine the intervals
Step 6: Pick a random number from each interval, substitute it into the inequality, and see if the inequality is satisfied.
Step 7: The solutions are the satisfied intervals.
However, we normally use algebraic operations like addition, subtraction, multiplication, and division to solve simple inequalities (linear).
Solving Inequalities by Adding
Inequalities are similar to equations. You must apply the same operation on the other side of the equation if you want to add or remove from one side of the equation.
Our goal while solving inequalities by adding is to have the variable stand alone. It’s the same as solving a math problem.
Adding numbers from both sides of the divide has no influence on the direction of the inequality. If the left and right sides of the equation are switched, the inequality’s direction will change. For instance, x<3 becomes 3>x. They’re the same thing; they’re simply written differently. You can use > or < when solving difficulties. It’s all down to your taste.
Solving Inequalities by Subtracting
Inequalities work in the same way that equations do. You must apply the same operation on the other side of the equation if you want to add or remove from one side of the equation. This guarantees that the inequality exists.
When solving inequalities by subtraction, we want the variable to stand alone. It could appear on the lower or upper end of the inequality scale.
The direction of the inequality is unaffected by subtracting a number from both sides of the inequality. The inequality’s direction will change if the left and right sides of the equation are flipped.
For instance, x < 3 will become 3 > x. They’re the same thing; they’re simply written differently. You can have the inequity pointing in either direction while solving problems. It makes no difference.
Addition and Subtraction Property
Inequalities have the addition and subtraction property, which states that adding or removing the same constant on both sides is equivalent.
Allow “m” to remain constant.
If x ≤ y, then x +m ≤ y+m
If x ≥ y, then x +m ≥ y+m
Similarly, in the case of subtraction,
If x ≤ y, then x -m ≤ y-m
If x ≥ y, then x – m ≥ y-m
Multiple Inequalities
It is possible to solve two inequalities simultaneously, just as it is possible to answer two simultaneous equations (or three, or four, etc.). The most crucial component of solving multiple simultaneous inequalities using multiplication or division is to solve each inequality separately before combining them.
- Solve each inequality independently.
- Combine each inequality and determine where they intersect (i.e., the areas where each inequality is satisfied—this area is the solution).
The given set of disparities is best conveyed graphically for many students. The overlapping graphical region is the solution to the collection of inequalities.
Division inequalities
The division property of inequality asserts that if one side of an inequality is divided by a number, the other side of the inequality is also divided by a number, the other side can be divided by the same number.
Multiplication and Division Property:
When both sides of an inequality multiply or divide a positive constant number, the inequality remains the same. The inequality expression will be reversed if it is multiplied or divided by a negative constant number.
Assume that “m” is a positive constant.
If x ≤ y, then xm ≤ ym (if m>0)
If x ≥ y, then xm ≥ ym (if m>0)
Assume that “m” is a negative constant number.
If x ≤ y, then xm ≥ ym (if m<0)
If x ≥ y, then xm ≤ ym (if m<0)
The above requirement holds true for the division operation.
Applications
Speed limits on roads, age limitations on certain movies, and the time it takes to go to the park are all examples of inequities. Inequalities do not indicate a precise number, but rather a limit to what is permitted or possible. Equal values are represented by equations.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






