Know About Solving a Line Graph

A line graph, also known as a line plot or a line chart, is a graph in which individual data points are connected by lines. A line graph shows quantitative values over a set period of time. Line charts are often used in finance to illustrate the price action of an asset or security over time.

Definition of Line Graph

A line graph is a sort of graph or chart that displays data that varies over time. A line graph is created by connecting numerous points using straight lines.

Basics of Line Graphs

The most efficient way to create a line chart is to:

The line chart has a vertical y-axis and a level x-axis. Line diagrams are drawn with the goal of placing dependent data on the vertical y-axis and autonomous data on the horizontal x-axis (e.g. time). Because the majority of line diagrams only deal with positive numbers, these axes frequently cross near the y-axis’ base and the x-axis’ left end. When the axes cross, it is more likely than not (0, 0). Each axis is labelled with a different information type. Days, quarters, weeks, or years, for example, could be on the x-axis, while income, generation, consumption, cost in rupees, and so on could be on the y-axis.

Line charts are useful because they clearly show information factors and patterns. Line diagrams can help people anticipate the ramifications of information that hasn’t been captured yet. The most capable visual gadget for fund, showcasing, and diverse zones is this type of chart. It can also be used for climate monitoring, laboratory research, or any other task that requires a relationship between two numerical data. If the diagram contains more than one line, it can be used to do a comparison between them. Line diagrams are only useful for contrasting these informational collections if the axes have identical scales.

Line Graph – Data Interpretation for CAT

Data interpretation, as the name implies, is all about logically interpreting data and answering questions. In the third section of the CAT, data interpretation is given the same weight as reading comprehension or geometry and algebra in the verbal section. CAT has had roughly 20 questions on data interpretation for the past two years (CAT 2014 & CAT 2015). If you haven’t taken this topic seriously yet, there is no better time than now to begin!

Tables, bar graphs, line graphs, paragraphs, and pie charts are just a few examples of how data can be represented. This post will focus on LINE GRAPHS and will teach you the fundamentals of a line graph.

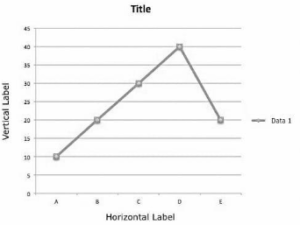
The following is a basic example of a line graph, with its numerous components:

The graph’s title informs us about what the graph is about.

Horizontal and vertical labels inform us about the data type.

Axis: The X and Y axes indicate the data’s unit.

Dots: The dots on the line graph represent a combination of data on the X and Y axes.

Line: In the graph above, the blue line connecting the dots represents the data and its variation visually.

Examine the graph below for its various components

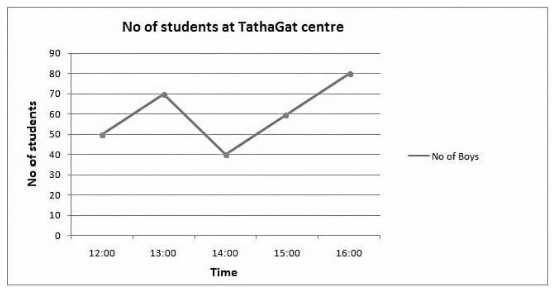
The graph is titled “Number of students at TathaGat centre.”

Label: “Time” is represented horizontally, and “Number of students” is represented vertically.

Axis: The X axis depicts time in hours, while the Y axis depicts an absolute number.

Dots: Dots reflect the number of boys at TathaGat at any given time. At 12 o’clock, there were 50 lads at TathaGat centre.

Line: That  line for boys depicts how the number of pupils rises from 12:00 to 13:00’o clock, drops to 40 at 14:00’o clock, and then rises again until 16:00’o clock.

We may clearly deduce from the above graphic representation that as the line rises, the number of students rises, and as it falls, the number of students reduces. However, the above blue line can also tell us the rate of this increment or decrement, or in other words, the data’s growth (positive or negative).

The slope of the line is directly proportional to the rate of increase or decrease. The steepness or inclination of the line is referred to as slope. Growth is related to the steepness of the line that is being followed. A thicker line indicates faster growth. So far, we’ve seen line graphs with only one variable or data; here’s an example of a line graph with two variables.

Examine the graph and its various components carefully and respond to the following question

Q1. At what time the number of boys was highest at the centre?

Solution 1: Based on the graph, it is clear that the number of boys was highest at 16:00 o’clock.

Q2. At what time the total number of students was lowest at the centre?

Solution 2: To determine the answer to this issue, add  the number of boys and girls at various hours.

At 12:00 o’clock total number of students = 90

At 13:00 o’clock total number of students = 130

At 14:00 o’clock total number of students = 110

At 15:00 o’clock total number of students = 110

So the answer is that the number of pupils was highest around 13:00 o’clock.

Q3. During what period the rate of growth of the numbers of girls were highest?

Solution 3: Looking at the graph, we can see that the red line is steepest between 12:00 and 13:00, indicating that this is when the number of girls is growing the fastest.

We may check it using the following formula:

Between 12:00 and 13:00, 13:00 and 14:00, 14:00 and 15:00, and 15:00 and 1600, the growth rate is 50 percent, 16.66 percent, – 28.56 percent, and -40 percent, respectively.

Conclusion

The main purpose of a line graph is to track changes over time, both short and long. It’s also utilised to compare changes in different groups during the same time period.