A cube or cuboid is a three-dimensional shape with six faces, eight vertices, and twelve edges. The main distinction is that a cube has all of its sides equal, whereas a cuboid has varying length, breadth, and height. Both shapes appear similar yet have distinct features. The area and volume of a cube, cuboid, and cylinder are all different.
Many objects, such as a wooden box, a matchbox, a tea packet, a chalk box, a dice, and a book, have been observed in ordinary life. These things all share the same shape. Six rectangular or square planes make up each of these things. These objects have either a cuboid or a cube shape in mathematics. With the help of their properties and formulas for surface area and volume, we will discover the difference between cube and cuboid shapes in this article.
Cube and Cuboid Shape Definition
In mathematics, the cube and cuboid are three-dimensional shapes. The cube and cuboid are formed by rotating two-dimensional geometries known as square and rectangle, respectively.
Cube is a three-dimensional shape described by the XYZ plane. Six faces, eight vertices, and twelve edges make up this hexagon. All of the cube’s faces are square and have the same measurements.
Cuboid: A polyhedron with six faces, eight vertices, and twelve edges is known as a cuboid. The cuboid’s faces are parallel. A cuboid’s faces, however, are not all the same size.
As a result, the cube and cuboid have six faces, eight vertices, and twelve edges.
Cube vs. Cuboid: What’s the Difference?
The following are the differences between the cube and cuboid shapes:
- The sides of a cube are equal, however they are not for cuboids.
- The sides of the cube are square, whereas the sides of the cuboid are rectangular.
- The cube’s diagonals are all equal, whereas only parallel sides of a cuboid have equal diagonals.
Cuboid Characteristics
The cuboid’s attributes, including its faces, base and lateral faces, edges, and vertices, are listed below.
Cuboid’s Faces
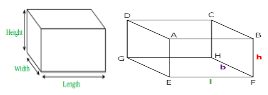
A cube is made up of six rectangles, each of which is referred to as a face. The 6 faces of the cuboid are ABFE, DAEH, DCGH, CBFG, ABCD, and EFGH in the diagram above.
A pair of opposed faces is formed by the top face ABCD and the bottom face EFGH. DAEH, CBFG, and ABFE, DCGH are also pairs of opposite faces. Adjacent faces are any two faces that are not opposite each other.
Consider the faces ABFE, BCGF, CDHG, and ADHE, which are adjacent to ABCD.
Faces on the Bottom and Sides
The base of a cuboid can be any face of the cuboid. The lateral faces of the cuboid are the four faces that are next to the base. The base of a solid is usually defined as the surface on which it sits.
The base of a cuboid is represented by EFGH in Figure 1.
The cuboid’s edge is a line segment connecting any two adjacent vertices.
AB, AD, AE, HD, HE, HG, GF, GC, FE, FB, EF, and CD are the 12 edges of a rectangle, and the opposite sides of a rectangle are equal.
AB = CD = GH = EF, AE = DH = BF = CG, and EH = FG = AD = BC are the results.
Cuboid’s Vertices
The vertex of a cuboid is the place where the three edges of the cuboid intersect.
There are eight vertices in a cuboid. In figure 1, the vertices A, B, C, D, E, F, G, and H depict the cuboid’s vertices.
The twelve edges of a cuboid can be divided into three groups by observing that all edges in one group are the same length, resulting in three separate groups termed length, breadth, and height.
A cube is a solid with the same length, width, and height in all three dimensions. A cube is a solid that is bordered by six square planar regions, with the edge being the cube’s side.
Cube Characteristics
Six faces and twelve equal-length edges make up a cube.
Its faces are square in form.
In the plane, the angles of the cube are right angles.
Each face of the cube comes into contact with four other faces.
Three faces and three edges meet at each vertex of the cube.
The cube’s opposite edges are parallel to one other.
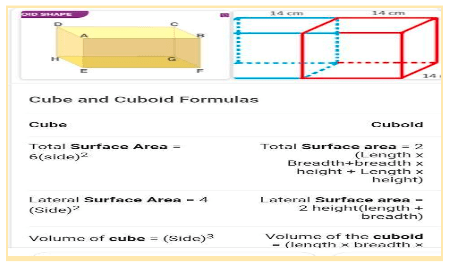
Cube and Cuboid Surface Area
The sum of the areas of a cuboid’s six rectangular sides equals its surface area.
Consider a cuboid with dimensions of ‘l’ cm in length, ‘b’ cm in width, and ‘h’ cm in height.
Face region ABCD = (l b) cm2 EFGH = Area of Face
Face region Area of face (BFGC) (b h) cm2 = AEHD
Face region Area of face (DHGC) ABFE = cm2 (l h)
A cuboid’s total surface area is equal to the sum of its six rectangular faces.
Total Cuboid Surface Area = 2(lb + bh +lh)
Find the total surface area of a cuboid whose length, breadth, and height are 5 cm, 3 cm, and 4 cm, respectively.
Given: l = 5 cm, b = 3 cm, and h = 4 cm in length, width, and height.
TSA = 2(lb + bh + lh) total surface area
= 2(5 × 3 + 3 × 4 + 5 × 4)
= 2(15 + 12 + 20)
= 2 (47)
= 94 sq.cm.
Cuboid’s Lateral Surface Area
The lateral surface area of a solid is defined as the sum of the surface areas of all faces except the top and bottom faces.
Consider a Cuboid with the dimensions of l, b, and h, respectively.
The cuboid’s lateral surface area equals its face area. ADHE + Facial Area BCGF + Facial Area ABFE + Facial Area DCGH
=2(b × h) + 2(l × h)
=2h(l + b)
Cuboid LSA = 2h(l +b)
Find the lateral surface area of a cuboid whose length, breadth, and height are 5 cm, 3 cm, and 4 cm, respectively.
Given dimensions of 5 cm in length, 3 cm in width, and 4 cm in height
LSA = 2h(l + b)
LSA = 2 × 4(5 + 3)
LSA = 2 × 4 (8)
LSA = 2 × 32 = 64 cm2
Cube’s Surface Area
The length, breadth, and height of a cube are equal.
Assume that the length of an edge is l.
As a result, the cube’s surface area = 2(l× l +l ×l +l ×l) = 2 x 3l2 = 6l2
The Cube’s total surface area is 6l2.
For example, if the cube’s side length is 6 cm, calculate its entire surface area.
Given that the side length is 6 cm
6l2 TSA of the cube
TSA = 6× (6)2
TSA = 6 × 36
TSA = 216 sq.cm
Cube with Cuboid Diagonal
The cuboid’s diagonal length is calculated as follows:
(l2 + b2 + h2) is the cuboid’s diagonal.
The length of a cube’s diagonal is given by:
a cube’s diagonal = √3l
Cube and Cuboid Perimeter
The cuboid’s perimeter is determined by its length, width, and height. Because the cuboid has 12 edges, each of which has a different value, the perimeter is calculated as follows:
A cuboid’s perimeter is equal to 4 (l + b + h).
where l stands for length
The width is b.
h stands for height.
Find the perimeter of a cuboid whose length, width, and height are 5 cm, 3 cm, and 4 cm, respectively.
Given dimensions of 5 cm in length, 3 cm in width, and 4 cm in height
4 (l + b + h) = 4 (5 + 3 + 4) Perimeter
P = 4 (12)
P = 48 cm
The perimeter of the cube is also determined by the number of edges and their length. Because the cube has 12 edges of equal length, the perimeter of the cube is calculated as follows:
A cube’s perimeter is 12l.
where l denotes the length of the cube’s edge
For example, if the cube’s side length is 6 cm, calculate its perimeter.
Suppose l = 6 cm.
12l is the cube’s perimeter.
P = 12 × 6
P = 72 cm
Conclusion
A cube or cuboid is a three-dimensional shape with six faces, eight vertices, and twelve edges. The main distinction is that a cube has all of its sides equal, whereas a cuboid has varying length, breadth, and height. Both shapes appear similar yet have distinct features. The area and volume of a cube, cuboid, and cylinder are all different .
Many objects, such as a wooden box, a matchbox, a tea packet, a chalk box, a dice, and a book, have been observed in ordinary life. These things all share the same shape. Six rectangular or square planes make up each of these things. These objects have either a cuboid or a cube shape in mathematics. With the help of their properties and formulas for surface area and volume, we will discover the difference between cube and cuboid shapes in this article.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out