Tangents

Through this article, we’ll learn about tangents. A tangent is a line that simply touches a curve or a circle from the outside. It is solely by means of tangent that we can articulate the slope of a curved function. We’ll also be discussing the properties of a tangent. The role tangent plays in geometry. And the theorems made on a tangent. We’ll see how a tangent is expressed through a formula. We’ll also see some real-life examples of tangents.

Meaning of tangent

‘Tangere ‘is the Latin word for tangent meaning ‘to touch.’ In simple words, a tangent is a line that touches the circle or any curve function at a single point. It does not intersect the circle at more than one point. It does not enter inside the circle. A tangent is a circle that forms a perpendicular with a radius. For a circle, there can be as many tangents as there are points in its circumference.

Let’s define a tangent

According to Leibniz, a tangent is defined as ‘the line through a pair of infinitely close points on the curve.’

Tangent in geometry

It is a line that touches the circle or a curved function at a single point from outside.

Line touching the point at A is the tangent.

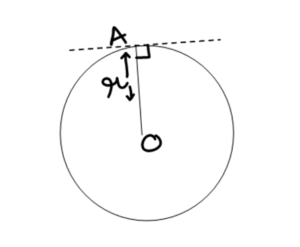
O is the centre of the circle.

 R is the radius of the circle.

A is the point of tangency

Tangent in trigonometry

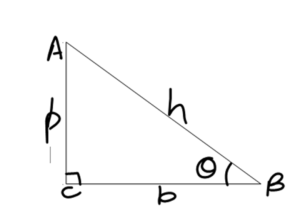
Tangent definition in terms of trigonometric functions. In a right-angled triangle ABC. With sides p, h, and b and angle theta. The tangent of an angle is expressed as:

Tanθ = perpendicular/ base

Formula for tangent

Tan theta = p/b

In terms of secant, a tangent is expressed as:

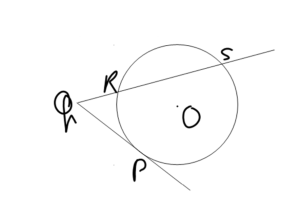
O is the centre of the circle. Q is the external point with respect to the circle. A line through Q intersects the circle from the outside at a point P. This line is the tangent. Another line through Q intersects the circle from inside at two points, R and S, respectively. This line is called a secant. So, according to the formula:

  QS/QP = QP/ QR

           QP² = QR. RS

Some properties of tangents.

1. a) A tangent is a line emerging from an exterior point of a circle. It does not cross the circle. It only touches the circle from a point outside.
2. b) At the touching point of the tangent, it forms a perpendicular with the radius of the circle.
3. c) Tangent segments to a circle are equal from the same external point.

Tangent theorems

Theorem 1

A radius is obtained by joining the centre and the point of tangency. The tangent at a point on a circle is at right angles to this radius. As depicted in the diagram below

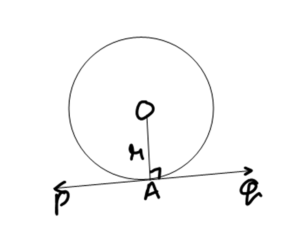
O is the centre of the circle

r is the radius of the circle

PQ is the tangent

A is the point of tangency

Theorem 2

According to this theorem, if from one external point, two tangents are drawn to a circle, then they have equal tangent segments. (Tangent segment refers to AP and AQ here. The line joins the external point to the point of tangency). It is depicted in the diagram below

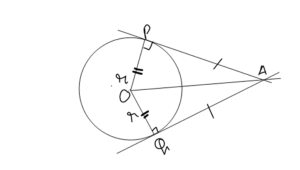
PA is a tangent

QA is a tangent

O is the centre

r is the radius of the circle

Tangent in real life

1. The most common example of a tangent is a bicycle tire. As the bicycle moves on the road, each point on the circumference of the tire makes a tangent with the road.
2. When weight or stone is tied to a string and rotated in a circular motion. It follows a circular path. If we let go of the weight/stone, its path can be described as a tangent to the circle.

Conclusion

A tangent is a straight line that touches the circle at an outside point. The word tangent is derived from the Latin word tangere. It is perpendicular to the radius of the circle. In terms of trigonometry, it is denoted as perpendicular/ base in relation to the right-angled triangle with an angle theta. It is also defined in terms of the secant of the circle. Tangents play an important role in finding the slope of a curved function. Tangents in real life can be mentioned while bicycling. At the points where the road touches the bicycle tire, it forms a tangent.