Profile
Settings
Refer your friends
Sign out
What is Relation?
A collection or conglomeration of order in a pair is termed a relation. The relation is used to connect an element or an object as well as two or more than two sets. We must note that the sets must not be empty set. One of the concepts is Equivalence Relation.
In simple words, a relation can be defined as a group of ordered pairs. A relation can be represented either by the set builder form or by an arrow diagram which is a visual representation of a relation or by the Roster Form.
A relation shows us a relationship between two given values. If we are provided with two sets- set P and set Q, then, a relation ‘R’ from P to Q is then a subset of the Cartesian product of PxQ and is then derived by defining a relation between the first element (p) and the other element (q) of the ordered pairs in P and Q.
Consider an example of two sets, A = {1, 2, 3, 5, 7, 12, 11} and B = {2, 5, 3, 7, 15}. Cartesian product P × Q has 30 ordered pairs such that P × Q = {(1, 2), (2, 5)…(12, 15)}. From this, we can obtain a subset of P × Q, by introducing a relation R between the first element and the second element of the ordered pair (p, q) as- R = {(p, q): p = 4q – 3, p ∈ A and q ∈ B}.
Then, R = {(1, 2), (2, 5), (12, 15)}.
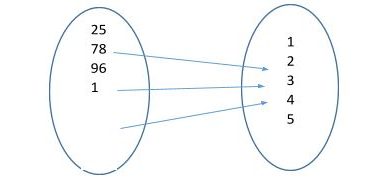
Representation of a Relation
A relation is depicted by Set-builder method or by the Roster method. Consider an example of two sets P = {1,2, 3} and Q = {2, 4, 9, 16, 25, 36}. It is noticed that the relation between the elements of set A are the squares of the elements of set B.
Some Important Key Definitions-
Domain: The set of all first elements of the ordered pairs in a relation R from a set A to a set B.
Range: The set of all the second elements of a relation R from a set A to a set B can be called a range.
Co-domain: The whole set B, that is the range ⊆ co-domain.
Equivalence relation
A relation ‘R’ of a set A is said to be an equivalence relation if and only if the relation ‘R’ is reflexive, symmetric, and transitive. The equivalence relation is a relationship of the set which is often represented by the transverse symbol “∼”. In easy language, A relation will be known as equivalence relation if it satisfies the properties of symmetric, transitive, and reflexive.
- Reflexivity is shown when- a ∼ a,
- Symmetry is shown when- a ∼ b then b ∼ a,
- Transitivity is shown when- a ∼ b and b ∼ c then a ∼ c.
Equivalence relations are used to group objects that are identical or similar.
Example: The relation “is equal to”, is denoted by an “=”, is an equivalence relation on the set of real numbers since for any x, y, z ∈ R:
- Reflexivity when x = x,
- Symmetry when x = y then y = x,
- Transitivity when x = y and y = z then x = z.
All of these are true.
Types of Relations-
Empty Relation: A relation R on a set A is called empty if set A is an empty set.
R = Ø
Universal Relation: In a universal relation, all the elements of set A have a relationship with all the elements of set B. Thus, this relation is called a universal relation.
Identity Relation: All the elements of set A have a relation with itself only in identity relation.
A: A → A
Inverse Relation: Let us take this under the assumption that there are two sets,namely set A and B, and they have a relation from A to B. This relation will be then described as R ∈ A×B. The inverse relation is only obtained when we change the first element of each given pair with the second element of a given set.
R-1 = {(b, a) : (a, b) ∈ R}
Reflexive Relation: A relation is called as a reflexive relation if all the elements of set A are related to itself. The word reflexive has a meaning that in a given set, the image of all the elements has their own mirror image.
Symmetric Relation: Let us suppose that there are two elements in set A, namely, b and c. The relation of a set A will be called as symmetric relation only if all the elements of ‘b’ have a relation with ‘c’, then ‘c’ also has a relation with ‘b’.
If (b, c) ∈ R then (c, b) ∈ R, for all b and c belongs to A
Asymmetric Relation: Relation of setA is said to be Asymmetric.
If (x,y) ∈ R then (y,x) ∈ R ∀ x,y ∈ A
If xRy then yRx
Transitive Relation: Let us suppose there are three elements in a set A, namely, p, q, and r. The relation on a set A will be called a transitive relation if and only if ‘p’ has a relation with ‘q’ and ‘q’ has a relation with ‘r’, then ‘p’ will also have a relation with ‘r’. The transitive relation is described as follows.
If (p, q) ∈ R , (q, r) ∈ R , then (p, r) ∈ R for all p, q, r ∈ A
