Factorial Permutation

Introduction

It can be stated that the factorials are numbers that have the exclamation mark (!) after them and permutation is defined as a numerical method that is used to determine the figure of all achievable arrangements at a given set in the event when the arrangements are done of those given sets matter. When we encounter n!. The factorial is the actual product of all the whole numbers between a and n (known as the ‘n’ factorial) where n is always positive. Factorial permutations are often disoriented with different numerical methods known as combinations. It must be noted that in the case of these mixtures the way in which the items are chosen cannot be influenced at all. For example, if we consider the arrangements; ab and ba in permutations, they will be considered as various arrangements, in the case of combinations, the same arrangements will be considered as equal. This mathematical technique allows us to understand the available motions we have and what kind of arrangement will be best suited to get the desired result when a set of elements are given. 

Permutation Formula

To understand this mathematical technique, which is used to determine the number of all the possible arrangements that can be formed in a given set during a situation when the order of those arrangements will matter, a formula will be necessary. The general formula of permutation can be expressed as;

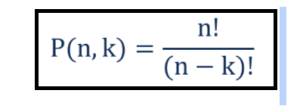
Where, 

n = the overall sum of elements that are included in a group

k = selected component which is displayed at a particular manner numerically

! represents that it is factorial (The factorial is noted by the exclamatory sign which means it is the item of all practical integers which are either lesser than or as equal as the number which follows the factorial sign. Example 3! represents 1*2*3= 6. 

The above-mentioned formula of permutation can be utilized in times when several components from a group are to be selected and are to be arranged at a specific or special order. 

Factorial Notations

The factorial notation is a way to find the factorial value of the positive natural numbers. The factorial notation of a natural number ‘n,’ is denoted as n!. Factorial of n can be represented by n! = 1*2*3…. (n-2) * (n-1) * n. In most cases, the factorial notation is used in the formulas of permutation and also in the formulas of combination. In factorial notation, the factorial of a natural number is equal to the result of each natural number in the sequence from 1 to n. For example, if the factorial of the number 7 is written as 5! and is equal to 5*4*3*2*1.

Conclusion

As mentioned earlier, it must be noted that the factorial is the multiplicative product comprising all the whole numbers between a and n (known as the ‘n’ factorial) where n is always positive. Factorial permutations are quite similar to combinations and they are often confused with combinations. The main differentiating factor between permutations and combinations is that in the case of combinations, the selection remains uninfluenced by the chosen selection order. For example, in the arrangements; ab and ba in permutations, they will be considered as different arrangements, while in the case of combinations, the same arrangements will be considered as equal. Factorial proof can be done using the factorial notation and factorial formula and this technique is essential for a variety of uses when different forms of arrangements in a given set of elements are given. With the help of this method, the number of potential decisions that can be made so that the most desirable result can be achieved and the most efficient method to gain that is used in the process. Other than that, another core use of this method is to figure out the most appropriate order or arrangement from a given set (which can vary in terms of quantity).