Applications Of Integral Calculus

Introduction

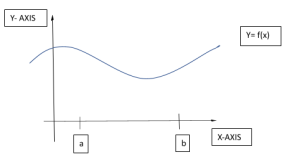
Here we have a curve we are denoting by y=f(x). Now if we are asked to find the area under the curve or more precisely the area under the curve and above the X-Axis, which in essence boils down to the area between two fixed boundaries, x=a and x=b. Now one way to go at this is by dividing the said area into tiny rectangles of ∆x1 to ∆xn. Now the area of all these rectangles will be –

Fxix ∆xi  

Now what we have is our area that we can make as approximately close to the actual area by increasing the value of n which would do nothing but make our rectangles thinner and thinner. This is the core idea of Integral Calculus. 

i=1nf(xi) ∆x1 = abfxdx

Here we can view the integral sign as the summation sign, but instead of taking the sum of discreet number of things we are taking the sum of infinitely many number of thin rectangles. Instead of ∆x we now have dx.

FORMULAS OF INTEGRAL CALCULUS 

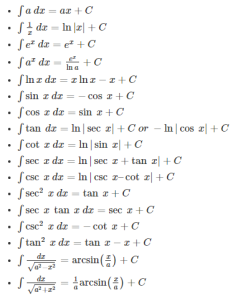
FUNDAMENTAL THEOREM OF INTEGRAL CALCULUS-

Anytime we wish to integrate some function where we are adding up the values of abfxdx for inputs in a certain range and then asking what does that sum approach as dx approaches zero? The first step to evaluating that integral is to find the anti-derivative of another function F whose derivate is what’s inside the integral. Then the integral equals that anti-derivative evaluated at the value of its top bound ‘b’ minus the value of its bottom bound ‘a’. And this fact is nothing but the fundamental theorem of calculus.

Mathematically,

dF(x)dx= f(x) and abfxdx= F(b)-F(a)

APPLICATIONS OF INTEGRAL CALCULUS –

As mentioned previously, integral calculus helps us in finding the area between two curves but that’s not all that its used for. Its applied while finding the speed, distance, acceleration of moving bodies, volume, surface area etc. Let us now suppose an example to understand the application better.

Imagine that you are sitting in a car and hypothetically can’t see out of the window. Whats visible to you is only the speedometer. At some point the car starts moving. Speeds up and then slows down to a stop all over the course of 20 seconds. Now is there a way for us to calculate how far we have travelled only by reading the numbers on the speedometer? Or can we find a distance function d(t) that tells us how far we have travelled in the given amount of time t, somewhere between 0 and 20 seconds? Lets say we take note of the velocity at every second and plot it over time. What we will basically be doing is, we will find the anti-derivative of the velocity function over time to find the distance.

A student can question – why did we simply not multiply the velocity with the time to get the distance? The answer to the question would be that since the car is not moving with a uniform velocity the formula Speed = distancetime wouldn’t work.

This is basically what area under the curve teaches us. By adding up the area bounded by t=0 to t=20 using integration we will be able to find the correct distance travelled by the car.

CONCLUSION

Integral calculus is  very essential for calculating the anti- derivative of various functions. It is used in different subjects like physics , chemistry , biotechnology, etc for estimating different quantities. This is basically used to calculate the area under the curve.