Algebra of Matrices

A matrix is a set of numbers that are arranged in rows and columns (e.g., in the spreadsheet). It is used to show groups of data in mathematics or statistics. It is often helpful to solve practical problems. Understanding algebra of matrices can be hard and complex, but it is easier if you understand its concepts first.

Documentation

The algebra of matrices define how to write things in a particular way. When we write things differently, we do it because it’s more common than writing them in the format of a spreadsheet. People who follow arrangements find it easier to follow the matrix rules when they do maths (subtraction, Addition, Multiplication, and others). Here is an example: suppose you have a list of like:5 bananas, 2 grapes, and 3apples. It is easy to understand if you write it as 5b+2g+3a. This is what following a format means.

There are a few terms that you will find while working with the matrix. They are:

●  Row: horizontal values/entries in a matrix.

● Column: vertical values/entries in a matrix.

● Order: Commonly known as dimension or order. It means how the number of columns and rows are there in the matrix. Rows appear first and then columns. There are three rows and two columns in a 3 x 2 matrix.

●  Scalar: A scalar is a real number.

● Components:  The numbers which show up in the matrix are called elements.

● Matrix function: A scalar matrix is multiplied with a different matrix to make another matrix.

● Unit Matrix: Commonly known as Identity matrix(I). A matrix that has 0 as an element in all other positions but diagonally. All diagonal elements are 1. This is called a “diamond matrix.”

Algebra of matrices

Subtraction and Addition

It is called the matrix order or matrix dimension when the size of the matrix is (like 3 x 3). There must be the same number of rows and columns in each of two matrices when doing addition or subtraction. Add a 3 x 3 matrix to another 3 x 3 matrix. A 3 x 2 matrix can’t be added to a 3 x 3 matrix. The process of adding matrices is just the same as adding a lot of other things. Just add the numbers in the same position (add all numbers in row 1, column 1, and numbers inrow2, column 2).

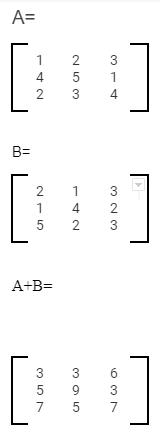
The subtraction of matrices is similar. The entire process works in the same manner as an addition.

Multiplication

A single-digit multiplication with a matrix is very easy. You just have to multiply the digit with every number in the matrix.

Multiply every number of matrices by 3 to get another matrix.

3 * 2 = 6

3 * 6 = 18

3 * 3 = 9

3 * 5 = 15

Two Matrices

There are some more steps when you want to multiply matrices. Multiply the columns of the second matrix by the rows of the first matrix to get the right answer for each row. If you want to do this, multiply rows-rows and columns-columns of the matrices. Then, after you have multiplied all the way through, add all the results together and make a new matrix.

Diagonal Matrix

If you make a symmetrical matrix that has all zeros except for the bottom right to top left diagonal, it is called a diagonal matrix.

A matrix with all zeroes is also a diagonal matrix.

The unit matrix with 1 in a diagonal position and all other values as 0 is called a diagonal matrix.

When n is the matrix order, that matrix can have n numbers that are not 0 diagonally. In a 2 x 2 matrix (order 2), there are 2 numbers on the diagonal. In a 3 x 3 matrix (order 3), there are 3 numbers on the diagonal.

Determinant of matrix

This is a type of special number that describes the matrix. It is used to find solutions to inverse matrices, linear equations and does other things in calculus and stats. There is no easy way to explain this in words. You can think about its uses in terms of maths. Several things make up the determinant of a matrix:

●  A real positive or negative number.

●  It is available for square matrices only.

Transpose matrix

Transpose matrix (or matrix transpose) is when you change all of the matrix rows into matrix columns. When you do complex Multiplication, this is very helpful.

Symmetrical Matrix

It is a type of matrix that is the same on both sides. As you can see below, the top left corner to the bottom right corner of a symmetric matrix is the same. Try to fold the matrix along the diagonal (don’t think about the numbers in the diagonal). Each half of the matrix is the same except the diagonal.

Augmented Matrix

This is an augmented matrix (A|B). It is used to solve linear equations, which is the reason for their origin. This is an “augmented matrix” because the values that follow the equals sign have been added to what’s already in the coefficient matrix.

Inverse Matrix

Inverse matrices are the same thing as reciprocals. In secondary school, you came to know of a reciprocal. When one number is multiplied by another, it can be equal to 1.

The reciprocal of 7 is 1/7

The reciprocal of 8 is 1/8

Conclusion

Matrices and their operations are complex to understand. You require a thorough understanding of the concepts to perform these operations. Find Algebra of matrices MCQ to check your knowledge. Matrices help solve real problems.