Mixture and Alligation

Two or more components are combined to create a new substance. When various quantities of different components are combined to generate a combination with a mean value, the ratio of their quantities is inversely proportional to the cost variations between the constituents. We can rapidly determine the cost of a combination by using an alignment rule. This rule allows us to blend two separate parts with varying costs.

Mixture and Alligation Formula

Alligation, as the name indicates, is the process of determining the ratio of the ingredients/things that have been blended and the price at which they are sold to generate profit or lose money.

Knowing how alligation is used to obtain the mean value of a mix when the ratio and amount of the substances blended are varied is essential to solving mixture and alligation issues.

The main formula in mixture and alligation is:

Quantity of Cheaper ∕ Quantity of Dearer = CP of dearer – Mean Price ∕ MP – CP of cheaper

When we have an initial quantity of a pure element (such as petrol), and we keep replacing a fixed part of this pure liquid with another element (such as water), we use the following formula to determine the quantity of pure element after ‘n’ replacements:

P x [1 – (R / P)]n

where P denotes the starting concentration of the pure element,

R is the quantity replaced each time, and

n denotes the total number of replacements.

Mixture and Alligation Questions

Question 1: From a vessel containing 20 litres of pure milk, 5 litres are removed and replaced with water to maintain a capacity of 20 litres. This procedure is performed five times more. Calculate the proportion of pure milk remaining in the vessel following five replacements.

Suggestion: In this case, we must use the formula P x [1 – (R / P)]n

P = 20 litres

R = Quantity replenished = 15 litre

n = 5

Thus, the quantity of pure milk after five substitutions is 20 x [1 – (15/ 20)]5

Quantity of pure milk following 5 substitutions = 20 x ¼ x ¼ x ¼ x ¼ x ¼ = 5/256

Thus, the proportion of pure milk remaining in the vessel following five replacements is calculated as 5 / 256 x 20 = 5/5120 x 100 = 500/5120 = 0.09765625% of pure milk.

Question 2: Thirty litres of a milk-water combination contain 10% water; how much water should be added to increase the water content to 25% in the new mixture? Calculate the volume of water that will be added.

Solution: The quantity of water in the mixture = 30 x 10/100 = 3 litres

Milk in the mixture = 30 x 90/100 = 27 litres

Let the water to be added be x.

Therefore, the water to be added will be (3 + x)/ (30 + x) = 25/100

100(3 + x) = 25(30 + x)

300 + 100x = 750 + 25x

75x = 450

x = 6

We will need to add 6 litres of water to the mixture.

Alternate Formula for Mixture and Alligation

Where c is the CP of 1 unit of the cheaper element,

d is the CP of 1 unit of the dearer element,

M is the mean price,

d – m is the quantity of the cheaper element, and

m – c is the quantity of the dearer element.

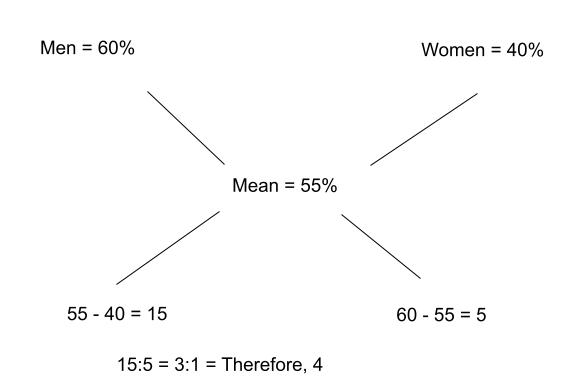
For example, a total of 25000 candidates took a test. 60% of men and 40% of women passed the exams. If the overall percentage of students that passed the test is 55%, how many females took the exam?

So, 25,000 students appeared in the exam.

25,000 x ¼ = 6,250

The number of girls that took the exam is 6,250.

Conclusion

A mixture is made up of two or more ingredients that combine to generate a third element. The combination questions are typically based on Ratio and Proportion and do not involve using any particular formulas.

Alligation is a mathematical method that helps us rapidly compute a mixture’s price when it consists of two parts with distinct costs. Alligation is the rule that enables us to determine the ratio in which two or more elements at a particular price must be combined to get the desired price mixture. The Mean Price of a unit amount of such a combination is the cost price of that unit quantity.

Bear in mind that the cost of the more expensive component > the cost of the mixture > the cost of the less expensive ingredient.