A rational nomenclature system must do at least two things. First, it should indicate how the carbon atoms of a given compound or molecules are bonded together in a characteristic lattice of chains and rings. Second, it should identify and locate any functional groups present in the given compound. Since hydrogen is such a common component in all kinds of organic compounds, its amount and locations can be assumed from the tetravalency of carbon, and need not be specified in most cases while naming a compound.
The IUPAC nomenclature system is a set of rules in organic chemistry. Knowing these rules and given a structural formula, one should be able to write a unique name for every distinct and different compound. Likewise, by giving an IUPAC name to someone, one should be able to write a structural formula. In general, an IUPAC name has three features.
• A root or base indicating a major chain or ring of carbon atoms found in the molecular structure of that compound.
• A suffix or other element(s) designating functional groups that may be present in the given compound.
• Names of the substituent groups, other than hydrogen, that complete the molecular structure of that compound.
Let us first consider compounds that have no specific functional groups in it. Such compounds are composed only of carbon and hydrogen atoms bonded together by sigma bonds in other words all carbons are sp3 hybridized.
IUPAC way to name alkyne
The most commonly used name for ethyne is acetylene, which used mostly used industrially. The nomenclature of alkynes have certain rules to follow which are discussed-
Rule 1
Find the longest carbon chain that includes both carbons of the triple bond in the given compound.
Rule 2
Now Number the longest chain starting at the end closest to the triple bond in the compound, A 1-alkyne is referred to as a terminal alkyne and alkynes at any other position are internal alkynes.
For example:
Rule 3
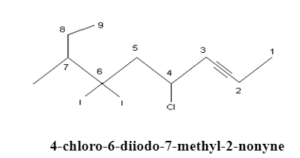
Now After numbering the longest chain with the lowest number assigned to the alkyne as functional group, label each of the substituents at its corresponding carbon. While writing out the name of the molecule, arrange the substituents and extra functional groups in alphabetical order, and If there are two, three, etc substituent in the compound use the prefixes di, tri, and tetra for two, three, and four substituents respectively. Please note that These prefixes are not taken into account in the alphabetical order.
For example:
If there is an alcohol present in the molecule, then number the longest chain starting at the end closest to the alcohol, and follow the same rules. However, the suffix would be –ynol, because the alcohol group takes priority over the triple bond in organic chemistry.
When there are two triple bonds in the molecule, find the longest carbon chain that includes both the triple bonds. Number the longest chain starting at the end closest to the triple bond that appears first in the given compound. The suffix that would be used to name this kind of molecule would be –diyne.
For example:
Rule 4
The Substituents containing a triple bond are called alkynyl
For example:
Rule 5
A molecule that contains both double and triple bonds is called an alkenyne. The chain must be numbered starting with the end closest to the functional group that appears first in the given compound.
For example:
If both the functional groups are the exact same distance from the ending of the parent chain, the alkenes takes precedence in the numbering of the compound.
Triple Bond:
When three pairs of electrons are shared between two carbon atoms, it is known as a triple bond between the two carbon atoms. The only distinguishing features of alkynes from the other hydrocarbons are the triple bond which exists between the carbon atoms in alkynes.
The triple bond atoms of carbon in acetylene are sp hybridized. Sigma bond between the carbon atoms is obtained by an overlapping of the two hybridized sp orbitals. The leftover orbitals of the carbon atoms overlap with each other along the internuclear axis in the 1s orbital of each hydrogen atom which results in the formation of one C-H sigma bond and 2 weaker pi-bonds in the molecule. These bonds are formed due to orbital overlapping in the molecule. Each carbon atom uses only one of its three p-orbitals for hybridization.
Hence, the two remaining p orbitals are occupied by a single electron in the carbon atom. As it is the same as the other carbon atom, it permits the pairing of electrons which results in the formation of 2 pi bonds in the molecule. The carbon-carbon triple bond is made stronger by the presence of a one sigma bond with it.
The Acetylene molecule is a linear molecule with a carbon-carbon distance of 1.21Ao. The C-H distance in acetylene is 1.08 shorter than that of alkenes due to the fact that sp hybridized carbon has more s character than a sp2 hybridized carbon.
Conclusion:
The Alkynes are organic compound consisting of carbon-carbon triple bonds and are written in the empirical formula in the form CnH2n−2. The IUPAC is short for for International Union of Pure and Applied Chemistry. It is the world authority on chemical nomenclature as well as terminology. Therefore, IUPAC nomenclature is basically a method of naming organic compounds according to certain rules which is used all over the world. When there are three pairs of electrons are shared between two carbon atoms, it is known as a triple bond between the two carbon atoms. The only distinguishing features of alkynes from the other hydrocarbons are the triple bond which exists between the carbon atoms in alkynes.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out